Determine as transformadas de Fourier dos sinais indicados na Figura
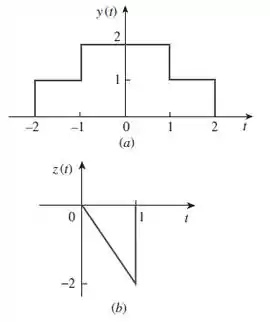
Passo 1
Galerinha, vamos pra letra (a)! Podemos expressar essa função da seguinte maneira:
Aplicando a transformada de Fourier:
Lembram dessa relação trigonométrica?
Assim,
Passo 2
Agora a letra (b). Podemos expressar essa função da seguinte maneira:
Aplicando a transformada de Fourier: