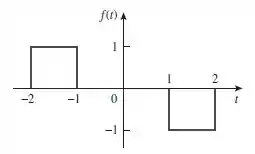
Obtenha a transformada de Fourier da função da Figura .
Passo 1
Galerinha, podemos ver no gráfico que a função é comporta por dois degraus unitários. Logo, vamos escrever a função no domínio do tempo:
Usando a propriedade do deslocamento e a tabela de Transformadas de Fourier, a transformada de Fourier da função é dada por:
Passo 2
Uma coisa maneira dos números complexos é que, com a ajuda deles, podemos escrever funções trigonométricas também. Por exemplo, o cosseno e o seno podem ser expressos como:
Vamos agrupar as exponenciais aqui na função para usarmos essas simplificações!
Sabemos já que . Vamos substituir esse valor na expressão:
Resposta
A transformada é igual a: