Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 15.Problemas - Ex. 23a
Determine as transformadas de Laplace das funções periódicas na figura
Passo 1
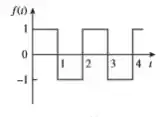
Bem, para começo de conversa, observe aqui que a função é periódica de período igual a :
Se a gente considerar como sendo apenas o trechinho que depois vai se repetir:
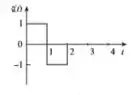
De acordo com a teoria de transformadas de funções periódicas, a transformada da função será:
Então agora temos que encontrar a transformada da função ! Bora?
Passo 2
A primeira coisa a se fazer aqui é construir essa em forma de degrau:
Esses números na frente de cada degrau são valores correspondentes ao tamanho do das barrinhas verticais. Por exemplo, em , temos um degrau de unidades (barra vertical), em , ele cai unidades (barra vertical), em ela sobe ficando eternamente , saca?
Então prontinho! Função descrita !
Passo 3
Finalmente podemos encontrar a Laplace dessa :
Como a Laplace da função degrau é...
Então...
Passo 4
Então, podemos falar que a transformada da função periódica é...