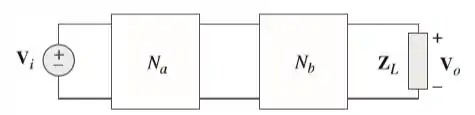
Para os dois circuitos de duas portas individuais indicados na figura onde
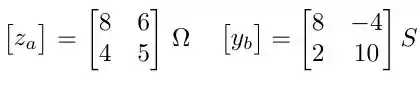
- Determine os parâmetros do circuito de duas portas global.
- Determine a relação de tensões quando .
Passo 1
Vamos considerar as matrizes:
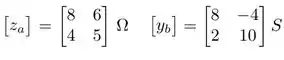
Convertendo os parâmetros em :
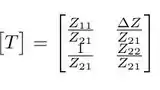
Então, a matriz é:
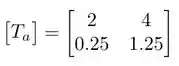
Passo 2
Vamos achar agora a outra parte dos parâmetros :
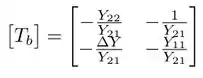
Então, a matriz é:
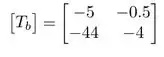
Passo 3
Para calcular a matriz :
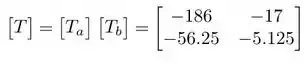
E agora, convertendo para parâmetros :
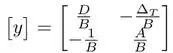
Então,
![]()
Passo 4
Na letra b, vamos converter os parâmetros em :
![]()
Passo 5
Em seguida nó fazemos o desenho para ficar mais claro:
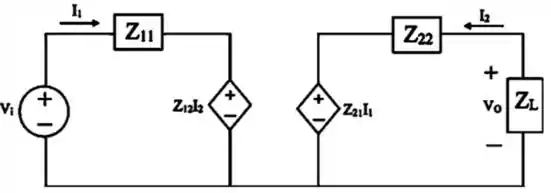
E agora a gente aplica a lei das tensões de Kirchhoff nos dois lados:
Lado esquerdo:
Lado direito:
Passo 6
Da figura temos a tensão que passa pela carga:
Substituindo por na equação
Chegamos em
Passo 7
Para calcular :