Elabore um problema para ajudar outros estudantes a entender melhor como determinar a tensão e a corrente em um elemento de circuito dadas as séries de Fourier da corrente e da tensão. Além disso, o problema também deve calcular a potência média fornecida ao elemento e o espectro de potência.
Passo 1
PROBLEMA: Para um circuito de painel de navio a tensão e a corrente vistos dos terminais de um gerador a óleo são dados:
- Calcule a tensão que sai do gerador.
- Calcule a potência média fornecida ao circuito e desenhe o espectro de potência.
Passo 2
Poxa, a tensão é dada pela fórmula:
Reconhece esse cara aí dentro da integral? Ele é o da Identidade de Parceval! Então devido a isso, podemos fazer essa substituição maravilhosa aqui:
Ora, no nosso caso, o nosso está representado apenas em cossenos...
Então (parte que representa o seno ):
representa a componente ...
Enquanto que , e representa os coeficientes na frente do cosseno:
Logo...
Passo 3
Aqui é um pouquinho diferente, lembre-se que potência sempre pode ser calculada usando Fourier dessa forma aqui:
Onde no nosso caso...
Temos que e as componentes de corrente contínua (os números soltos que não tem nesse problema)...
Já o somatório, depende das quantidades de frequências que se tem no problema no nosso caso, são cossenos das componentes de , e outro :
Então, como se tem três frequências diferentes, o nosso e a gente precisa determinar agora quem são e para cada uma das componentes de frequências:
Para ...
Já para não temos a componente de corrente, então...
Assim, podemos desmembrar o somatório dessa forma aqui:
Substituindo...
Pra desenhar o espectro de potência, repare que a parcela de energia correspondente ao é e a parcela correspondente de é , então...
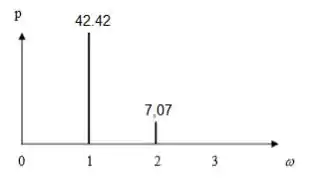
Resposta
Ei, a resposta está no passo a passo :)