Faça que e sejam conforme mostrado na figura a seguir. Determine .
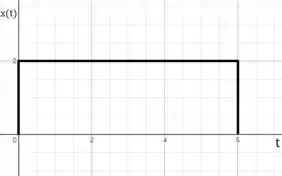
Passo 1
Para convoluirmos com , vamos pegar o gráfico de (que vem primeiro na operação) e “deslizar” pelo gráfico de , fazendo a integral de convolução em cada intervalo.
Vamos lá, o primeiro intervalo é , quando está completamente à esquerda de :
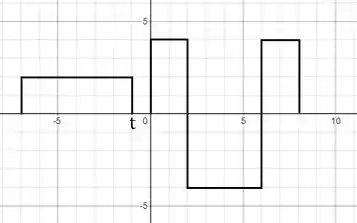
Nesse intervalo, não há sobreposição de com , então
Passo 2
Para o intervalo :
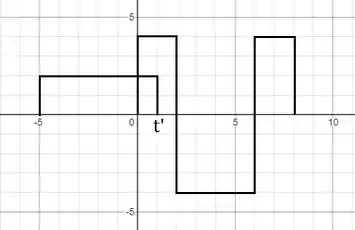
Nesse caso, há sobreposição dos gráficos de até , sendo que e , assim:
Lembrando: estamos usando como referência porque já representa o nosso eixo das abscissas. Mas no resultado final podemos trocar por .
Passo 3
Para o intervalo :
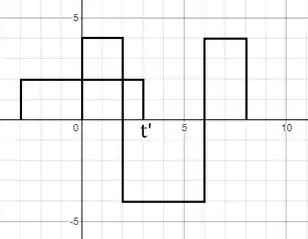
Agora, há sobreposição dos gráficos em (com e ) e depois em (com e ).
Então vamos somar as integrais nesses dois intervalos:
Passo 4
Para :
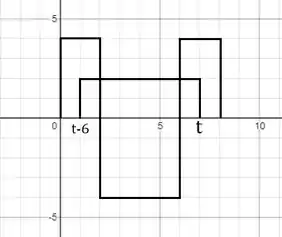
Há sobreposição em:
(com e )
(com e )
(com e )
Então vamos somar 3 integrais:
Passo 5
Para :
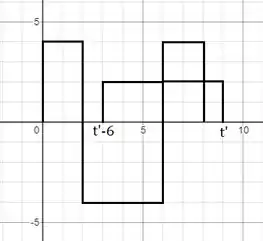
Há sobreposição em:
(com e )
(com e )
Observe que para , não há sobreposição.
Somando as duas integrais de convolução:
Passo 6
Para :
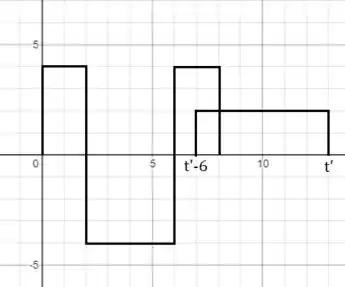
Há sobreposição em :
Para o gráfico de sai completamente de qualquer sobreposição com , logo, no caso, .
É isso aí, calculamos a convolução para todos os intervalos possíveis :D