A forma de onda de corrente periódica da figura é aplicada em um resistor de . Determine a percentagem de dissipação de potência média total provocada pela componente .
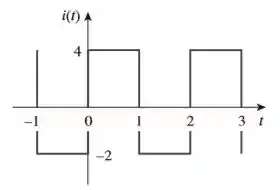
Passo 1
Pois bem, pela teoria de Fourier, podemos encontrar a componente de um sinal pela fórmula:
Percebendo que essa é uma função periódica de período e que ela possui definições diferentes de a e de a (ora é ora ele é ), podemos separar a integral em ...
Integrando...
E substituindo os intervalos...
Então é a componente . A potência média dissipada por ela é:
Passo 2
Já a potência média de toda a onda é dada por...
Onde...
Então, por substituição...
Substituindo-se a função e os limites de integração como fizemos anteriormente:
Integrando e substituindo-se os limites de integração...
Passo 3
Agora só falta fazermos o que se pede: determinar a relação entre a potência dissipada pela componente DC (que chamamos de ) e a potência média da onda ():
Então substituindo...
Ou seja, da energia total dissipada pela onda é dissipada pela componente DC.