Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 12
Uma função de transferência é dada por
Trace os gráficos de Bode de fase e amplitude.
Passo 1
A função de transferência precisa primeiro estar no formato de polos e zeros, para isso fatoramos o numerador e o denominador
Substituindo
Sendo assim possuímos 4 fatores na função de transferência
Passo 2
Nas resoluções de exercícios anteriores é fácil ver que o modulo de em pode ser expresso por
E a fase pode ser dada por
Resposta
O gráfico de amplitude é composto por fator a fator da amplitude em decibel
Logo teremos
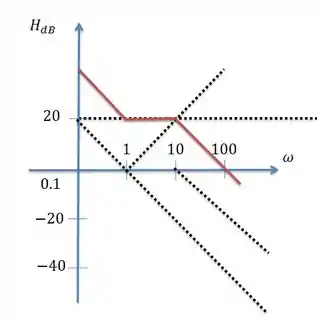
E o gráfico de fase
