Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 9
Um circuito em cascata apresenta um ganho de tensão de
Esboce os gráficos de Bode para o ganho
Passo 1
Gráfico de Bode é uma representação em função da frequência da amplitude em decibéis e da fase em graus de uma dada função de transferência
O legal do gráfico de Bode é que ele pode ser feito representando cada fator separadamente e então ir adicionando no gráfico.
Mas como é isso??? Vamos ver
Passo 2
Vamos partir primeiro pelo gráfico da amplitude
Nossa função de transferência pode ser simplificada um pouco mais, basta dividirmos ela por tanto em cima quanto embaixo. Assim oh
Resultando em
Dessa forma podemos representar a função fator por fator
Passo 3
A amplitude pode ser obtida por meio de
Passo 4
Como estamos tratando de logaritmo, este possui duas propriedades que podemos aplicar aqui. As propriedades são as seguintes
E
Passo 5
Sendo assim as amplitudes de podem ser obtidas por
Aplicando as propriedades do passo anterior
Ou ainda
Os polos simples e são as frequências de corte da função
Passo 6
Recorrendo a tabela 14.3 do livro podemos construir parte a parte do gráfico de Bode para a amplitude
Para que é um ganho teremos
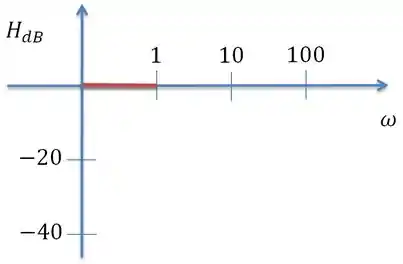
Pois
Para que possui polo simples igual a 1 pois é igual a
Em adição a obteremos
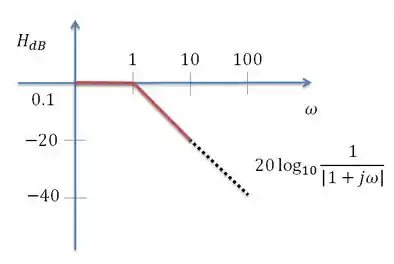
E por ultimo para que possui polo simples igual a 10. Obtermos a forma final para o gráfico de Bode para amplitude
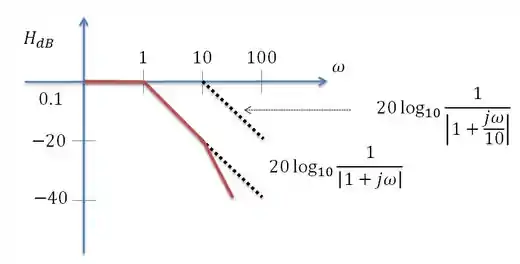
ATENÇÃO!!! Te atenta pro sinal dos fatores, que é só sucesso!!
Passo 7
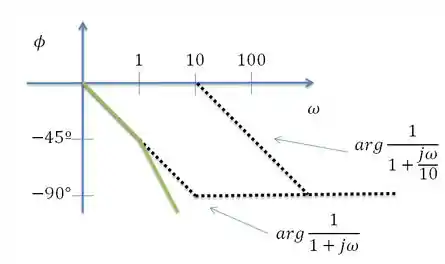
Para a fase o pensamento é parecido. Ainda em consulta a tabela 14.3
Para encontrar o ângulo de fase recorremos a expressão
Para o fator constante a fase será zero, então vamos partir pro fator com polo simples igual a 1
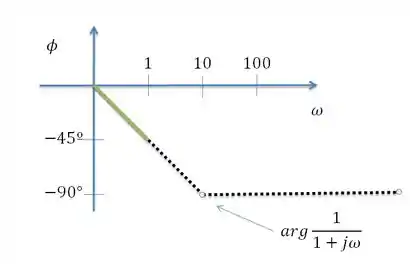
Com adição do fator com polo o gráfico final par a fase será
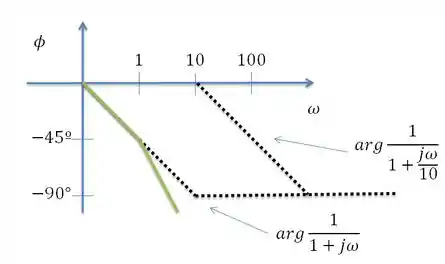
Resposta
Gráfico de Bode da amplitude
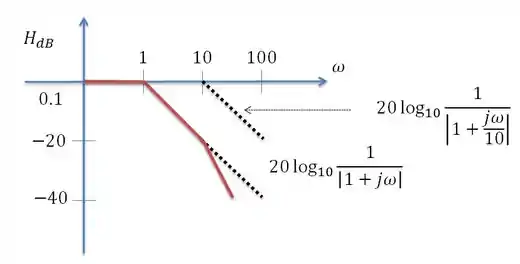
Gráfico de Bode da fase
