Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 69

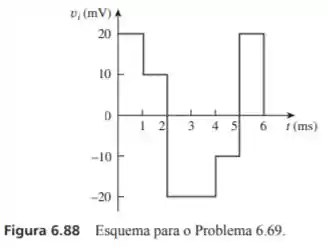
Um integrador com AOP e R = 4 M Ω C = 1 μ F tem a forma de onda mostrada na figura 6.88. Desenhe a forma de onda de saída.

Passo 1

Para facilitar as nossas contas, devemos reparar que como a nossa forma de onda não é descrita por uma regra geral, ou seja, por uma função que conhecemos, podemos trabalhar com intervalos onde ela é constante e podemos utilizar uma regra para defini-la. Além disso, devemos lembrar que a tensão de saída em um circuito integrador com amplificador operacional é regido pela seguinte equação

v 0 = - 1 R C ⋅ ∫ v i d t

Sendo assim, vamos dividir nosso seccionamento nos seguintes intervalos: 0 < t < 1 ,   1 < t < 2 ,     2 < t < 4 ,     4 < t < 5   e     5 < t < 6 .

Passo 2

Calculando a equação que vai regir a tensão de saída para cada intervalo vamos obter para 0 < t < 1

v 0 = - 1 4 ⋅ ∫ 0 t 20   d t = - 5 t   m V

Para 1 < t < 2  

v 0 = - 1 4 ⋅ ∫ 1 t 10   d t + v 1 = - 2.5 ⋅ t - 1 - 5 = - 2.5 t - 2.5 m V

Para 2 < t < 4  

v 0 = 1 4 ⋅ ∫ 2 t 2 0   d t + v 2 = 5 ⋅ t - 2 - 7 . 5 = 5 t - 17 . 5   m V

Para 4 < t < 5  

v 0 = 1 4 ⋅ ∫ 4 t 10   d t + v 4 = 2.5 ⋅ t - 4 + 2.5 = 2.5 t - 7.5   m V

Para 5 < t < 6

v 0 = - 1 4 ⋅ ∫ 5 t 2 0   d t + v 5 = - 5 ⋅ t - 5 + 5 = - 5 t + 30   m V

Juntando todas essas informações em um gráfico vamos obter

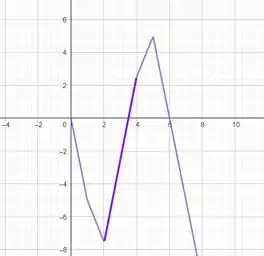
Resposta

Ver Outros Exercícios desse livro