Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 6.Problemas - Ex. 53

  1. Como mostra a perspectiva prática, o projeto de autocapacitância não permite uma verdadeira tela de múltiplos toques – se a tela é tocada em dois pontos, quatro locais de contato são identificados: dois reais e outros dois fantasmas. Se uma tela de toque de autocapacitância é tocada nas coordenadas x, y (2,1;4,3) e (3,2;2,5), quais são os quatro locais de toque a serem identificados? (Suponha que as coordenadas de toque são medidas em polegadas a partir do canto superior esquerdo da tela.)
  2. A tela de toque de autocapacitância ainda pode funcionar como uma tela multitouch para vários gestos comuns. Por exemplo, suponha que no instante t 1 os dois pontos de contato são aqueles identificados em (a), e no instante t 2 quatro pontos de contato associados às coordenadas x, y (1,8; 4,9) e (3,9;1,8) são identificados. Comparando-se os quatro pontos em t 1 com os quatro pontos em t 2 , o software é capaz de reconhecer um gesto de pinça – então, a tela deve ser reduzida ou ampliada?
  3. Repita a parte (b), supondo que no instante t 2 são identificados quatro pontos de toque associados às coordenadas x, y, (2,8;3,9) e (3,0;2,8).

Passo 1

Falaaa, pessoal! Como vocês estão?

Bora pra mais uma questãozinha pra exercitar o que a gente sabe sobre indutância e capacitância!

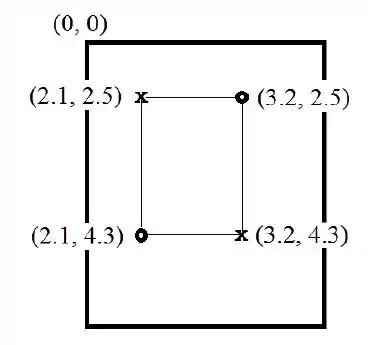
  1. O que devemos entender é que os quatro pontos de contato identificado são dois pontos reais e dois pontos fantasmas. Suas coordenadas, em polegadas são:

    2. 2,1 ; 4,3   3,2 ; 2,5   2,1 ; 2,5   ( 3,2 ; 4,3 )

    Essas quatro coordenadas formam um retângulo com a tela, como o mostrado abaixo:

    Passo 2

  2. Os pontos de contato identificados no tempo t1 são os listados no ítem (a). Já os pontos de contato reconhecidos no tempo t2 são:

    3. 1,8 ; 4,9   3,9 ; 1,8   1,8 ; 1,8   ( 3,9 ; 4,9 )

    Essas quatro coordenadas formam novamente um retângulo com a tela, como o mostrado abaixo:

  3. Os pontos de contato identificados no tempo t1 são os listados no ítem (a). Já os pontos de contato reconhecidos no tempo t2 são:

2 , 8 ; 3 , 9   3 , 0 ; 2 , 8   2 , 8 ; 2 , 8   ( 3 , 0 ; 3 , 9 )

Essas quatro coordenadas formam novamente um retângulo com a tela, como o mostrado abaixo:

Resposta

  1. 2,1 ; 4,3   3,2 ; 2,5   2,1 ; 2,5   ( 3,2 ; 4,3 )

  2. 1,8 ; 4,9   3,9 ; 1,8   1,8 ; 1,8   ( 3,9 ; 4,9 )

2,8 ; 3,9   3,0 ; 2,8   2,8 ; 2,8   ( 3,0 ; 3,9 )

Exercícios de Livros Relacionados

Determine as correntes I 1 , I 2 e I 3 no circuito da Figura abaixo. Determine a energia armazenada nas bobinas acopladas em t = 2m s . Adote ω = 1.000r a d / s .
Determine I X e V X no circuito da Figura 13.144 usando o PSpice ou MultiSim
Use o PSpice ou MultiSim para determinar V 1 , V 2 e I 0 no circuito da Figura 13.14 3 .
Determine I 1 , I 2 e I 3 no circuito do transformador ideal da Figura 13.14 5 usando o PSpice ou MultiSim