Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 20

Determine as correntes I 1 , I 2 e I 3 no circuito da Figura abaixo. Determine a energia armazenada nas bobinas acopladas em t = 2   m s . Adote ω = 1.000   r a d / s .

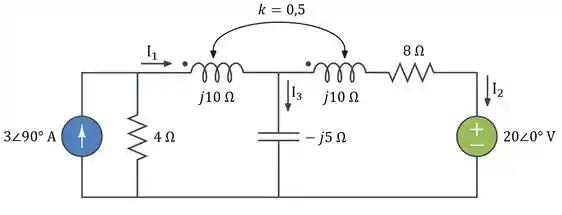
Passo 1

Primeiramente, vamos fazer uma simplificação no circuito transformando a fonte de corrente em paralelo com o resistor em uma fonte de tensão. O valor dessa fonte de corrente é calculado como se segue:

V = 3 ∠ 90 ° 4 = 12 ∠ 90 °   V = j 12   V

E o circuito equivalente é mostrado abaixo:

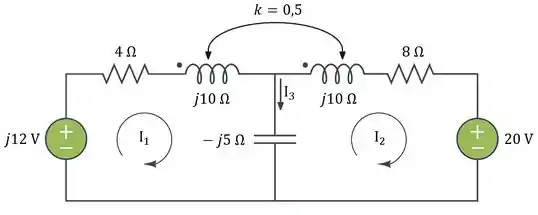
Passo 2

Vamos agora substituir o circuito acoplado mutuamente pela fonte dependente equivalente. Primeiro determinaremos as tensões induzidas e, em seguida, definimos os sinais adequados. Sabemos que:

j ω L 1 = j ω L 2 = j 10   ⇒   L 1 = L 2 = 10 ω

Com a relação de indutância mútua, obtemos o valor de ω M :

M = k L 1 L 2 = 0,5 100 ω 2 = 0,5 10 ω = 5 ω

ω M = 5

A corrente I 1 induz uma tensão na segunda bobina representada pelo valor j ω M I 1 , e I 2 induz uma tensão de j ω M I 2 na primeira bobina. Portanto, a tensão induzida na segunda bobina é j 5 I 1 e na primeira bobina é j 5 I 2 .

Para descobrir a polaridade da tensão mútua na bobina 1 devido à corrente I 2 , observamos que I 2 entra no terminal marcado com um ponto da bobina 2. Já que estamos aplicando a LKT no sentido horário, isso implica em uma tensão mútua positiva, isto é, j 5 I 2 . De forma similar, para descobrirmos a tensão mútua na bobina 2 em razão da corrente I 1 , observamos que I 1 entra no terminal marcado com um ponto da bobina 1, logo teremos uma tensão mútua positiva de j 5 I 1 .

Então o circuito equivalente com as fonte dependentes é mostrado a seguir:

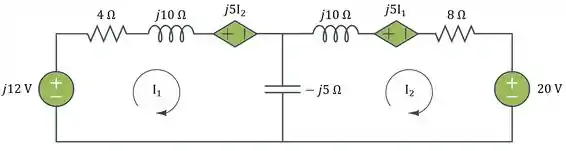
Passo 3

Para a malha 1 da Figura anterior, a LKT fornece:

0 = - 12 j + 4 + j 10 I 1 + j 5 I 2 - j 5 I 1 - I 2

j 12 = 4 + j 10 I 1 + j 5 I 2 - j 5 I 1 + j 5 I 2

j 12 = 4 + j 10 - j 5 I 1 + j 5 + j 5 I 2

j 12 = 4 + j 5 I 1 + j 10 I 2

Para a malha 2, temos:

0 = 20 - j 5 I 2 - I 1 + j 10 I 2 + j 5 I 1 + 8 I 2

- 20 = - j 5 I 2 + j 5 I 1 + j 10 I 2 + j 5 I 1 + 8 I 2

- 20 = j 5 + j 5 I 1 + 8 + j 10 - j 5 I 2

- 20 = j 10 I 1 + 8 + j 5 I 2

Colocando as equações das malhas na forma matricial, obtemos:

j 12 - 20 = 4 + j 5 j 10 j 10 8 + j 5 I 1 I 2

Passo 4

Os determinantes são:

∆ = 4 + j 5 j 10 j 10 8 + j 5 = 4 + j 5 8 + j 5 - j 10 ∙ j 10 = 7 + j 60 + 100 = 107 + j 6 0

∆ 1 = j 12 j 10 - 20 8 + j 5 = j 12 ∙ 8 + j 5 - - 20 j 10 = - 60 + j 96 + j 200 = - 60 + j 29 6

∆ 2 = 4 + j 5 j 12 j 10 - 20 = 4 + j 5 - 20 - j 10 j 12 = - 80 - j 100 + 120 = 40 - j 10 0

Portanto, obtemos as correntes de malha como segue:

I 1 = ∆ 1 ∆ = - 60 + j 29 6 107 + j 6 0 = 302,02 ∠ 101,46 ° 122,67 ∠ 29,28 ° = 2,46 ∠ 72,18 °

I 2 = ∆ 2 ∆ = 40 - j 10 0 107 + j 6 0 = 107,70 ∠ - 68,198 ° 122,67 ∠ 29,28 ° = 0,878 ∠ - 97,48 °

I 3 = I 1 - I 2 = 2,46 ∠ 72,18 ° - 0,878 ∠ - 97,48 ° = 0,75 + j 2,34 - - 0.11 - j 0,87

I 3 = 0,86 + j 3,21 = 3,32 ∠ 75 °

No domínio do tempo,

i 1 ( t ) = 2,46 cos ⁡ 1000 t + 72,18 °   A

e

i 2 ( t ) = 0,878 cos ⁡ 1000 t - 97,48 °   A

Em t = 2   m s , 1000 t = 2   r a d = 114,6 ° e

i 1 ( 0,002 ) = 2,46 cos ⁡ 114,6 ° + 72,18 ° = - 2,443   A

i 2 ( 0,002 ) = 0,878 cos ⁡ 114,6 ° - 97,48 ° = 0,839   A

Passo 5

A energia total armazenada nos indutores acoplados é:

w = 0,5 L 1 i 1 2 + 0,5 L 2 i 2 2 + M i 1 i 2

Sendo

ω L 1 = 10

ω = 1000   r a d / s

L 1 = L 2 = 10 ω = 10   m H

M = 0,5 L 1 = 0,5 L 2 = 0,5 × 10   m H = 5   m H

Logo:

w = 0,5 0,01 - 2,443 2 + 0,5 0,01 0,839 2 + 0,005 - 2,443 0,839

w = 0,0298 + 0,0035 - 0,0102

w = 0,0231 = 23,1   m J

Resposta

Portanto, as correntes I 1 , I 2 e I 3 são:

I 1 = 2,46 ∠ 72,18 °   A

I 2 = 0,878 ∠ - 97,48 °   A

I 3 = 3,32 ∠ 75 °   A

E a energia armazenada nas bobinas acopladas em t = 2   m s é :

w = 23,1   m J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere a Figura abaixo e elabore um problema para ajudar outros estudantes a entender melhor a energia em circuitos acoplados.
Detemrine I 0 no circuito da Figura 13.95 . Inverta o ponto no enrolamento da direita e calcule I 0 novamente.
Se M = 0,2H e v s = 12 cos ⁡ 10 tV no circuito da Figura 13.92 , determine i 1 e i 2 . Calcule a energia armazenada nas bobinas acopladas em t = 15m s .
No circuito da Figura 13.97 , determine o valor de X que resultará na máxima transferência de potência para a carga de 20Ω .
No circuito da figura 13.93 ,Determine o coeficiente de acoplamentoCalcule v 0 Determine a energia armazenada nos indutores acoplados em t = 2s .