Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 53
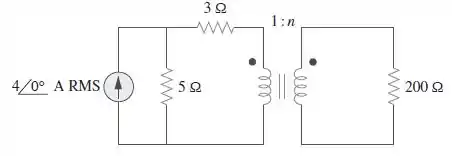
Observe o circuito da Figura .
- Determine para a máxima potência fornecida para a carga de .
- Determine a potência na carga de se .
Passo 1
Considere o circuito abaixo. A impedância de pode ser refletida para o lado primário!
Nós obtemos o equivalente de Thevenin do circuito conectado ao primário do transformador da seguinte maneira:
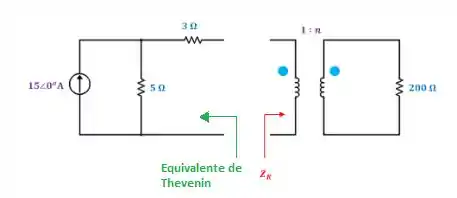
Para máxima transferência de potência, precisamos que a seguinte relação seja satisfeita:
Assim,
Passo 2
Mudar a relação não irá afetar o equivalente de Thevenin. O que será afetada é a impedância refletida do transformador. Para ,
Assim, a corrente que irá circular no circuito equivalente:
Assim, a potência média entregue à carga é igual a:
Resposta
A relação de espiras é igual a:
A potência na carga é:
Exercícios de Livros Relacionados
Para o circuito da Figura 13.126, determine I 1 ,I 2eV o .
Para o circuito da Figura 13.127, determine: A potência complexa fornecida pela fonteA potência média liberada para o resistor de 18Ω .
Determine as correntes de malha do circuito da Figura 13.128.
Para o circuito da Figura 13.129, determine a relação de espiras de modo que a potência máxima seja liberada para o resistor de 30k Ω .
Calcule a potência média dissipada pelo resistor de 20Ω na Figura 13.130.