Se três cópias do circuito da figura forem ligadas em paralelo, determine os parâmetros de transmissão globais.
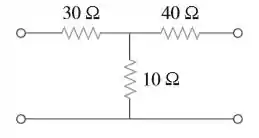
Passo 1
Vamos desenhar o circuito com os parâmetros indicados:
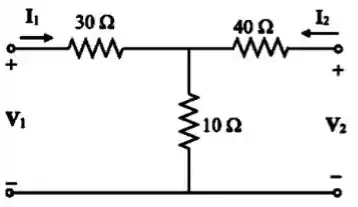
Passo 2
Definimos os parâmetros :
Para determinar aplicamos uma fonte de tensão e deixamos a saída aberta.
Aplicamos então a lei de Kirchhoff das tensões na malha de entrada:
Aplicamos também a lei de Kirchhoff das correntes no nó de cima:
E substituímos por chegando em:
Passo 3
Para determinar aplicamos uma fonte de tensão e deixamos a entrada aberta.
Aplicamos então a lei de Kirchhoff das tensões na malha de saída:
E
Então, a matriz é:

Passo 4
Para determinar os parâmetros , basta utilizar as seguintes fórmulas:
Substituindo todos os valores de que encontramos nos passos anteriores, teremos:
Passo 5
Para determinar os parâmetros das 3 cópias em paralelo, basta multiplicar cada um por 3:
Passo 6
Para converter os parâmetros para , utilizamos as seguintes fórmulas:
E então encontramos a matriz:
![]()
Resposta
![]()