Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 66
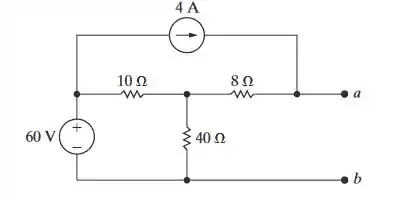
Obtenha o equivalente de Norton em relação aos terminais a, b para o circuito da Figura P4.66.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Primeiro, vamos encontrar o do circuito, para isso, no caso de obter a resistência , vamos definir a fonte de tensão como um curto-circuito e cada fonte de corrente como um circuito aberto, com isso, o circuito fica da seguinte forma
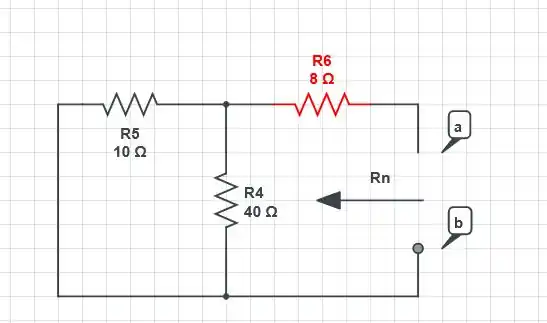
Logo, é igual a
Passo 2
Seja o circuito dado, vamos assumir um curto-circuito entre a e b, vamos considerar a corrente fluindo através da malha esquerda seja igual a e a da malha à direita sendo . Aplicando o método das correntes das malhas na malha esquerda
Rearranjando
Aplicando o método para a malha da direta, nós temos que
Novamente fazendo o rearranjo,
Resolvendo e nós obtemos os seguintes resultados
A corrente de Norton é a corrente que flui através do curto-circuito entre os pontos a e b, assim,