Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 55

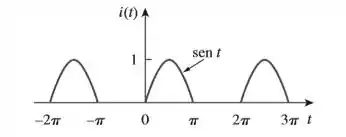
Obtenha a expansão da série de Fourier exponencial da corrente senoidal retificada de meia onda da figura.

Passo 1

De acordo com o nosso amigo Fourier exponencial, podemos obter c n (coeficientes da série de Fourier) através da integral:

c n = 1 T ∫ - T / 2 T / 2 f t e - j ω 0 n t   d t

No nosso caso, temos uma função de período T = 2 π , ou seja...

ω 0 = 2 π 2 π = 1

Substituindo então no c n ...

c n = 1 2 π ∫ 0 2 π f t e - j n t d t   →

A nossa função i tem diferente definições: de 0 a π ela é seno e de π a 2 π ela é 0 :

i t = sin ⁡ t ,           0 < t < π 0 ,                                 π < t < 2 π

Então... Como a nossa função tem definições diferentes...

c n = 1 2 π ∫ 0 π sin ⁡ t e - j n t d t + ∫ π 2 π 0 e - j n t d t   →

c n = 1 2 π ∫ 0 π sin ⁡ t e - j n t d t   →

Podemos calcular essa integral! Bora?

Passo 2

Lembrando que podemos escrever o seno em notação complexa assim...

sin ⁡ t = e j t - e - j t 2 j

Então...

c n = 1 2 π ∫ 0 π sin ⁡ t e - j n t d t   →

c n = 1 4 π j ∫ 0 π e j t - e - j t e - j n t d t   →

c n = 1 4 π j ∫ 0 π e j t - j n t - e - j t - j n t d t   →

c n = 1 4 π j ∫ 0 π e t j 1 - n - e t - j 1 + n d t   →

Integrando...

c n = 1 4 π j e t j 1 - n j 1 - n - e t - j 1 + n - j 1 + n 0 π   →

c n = 1 4 π j e π j 1 - n j 1 - n + e π - j 1 + n j 1 + n - e 0 j 1 - n + e 0 j 1 + n   →

c n = 1 4 π j e π j 1 - n - 1 j 1 - n + e π - j 1 + n - 1 j 1 + n →

Podemos simplificar isso um pouco passando esse j para fora e lembrando que j 2 = - 1 ...

c n = - 1 4 π e π j 1 - n - 1 1 - n + e π - j 1 + n - 1 1 + n →

Tirando um MMC...

c n = - 1 4 π e π j 1 - n - 1 1 + n + e π - j 1 + n - 1 1 - n 1 - n 1 + n →

c n = - 1 4 π 1 - n 2 e j π e - j n π - 1 1 + n + e - j π e - j n π - 1 1 - n →

c n = - 1 4 π 1 - n 2 e j π e - j n π + n e j π e - j n π - 1 - n + e - j π e - j n π - n e - j π e - j n π - 1 + n →

c n = - 1 4 π 1 - n 2 e j π e - j n π + n e j π e - j n π + e - j π e - j n π - n e - j π e - j n π - 2 →

Lembre-se e - j π = cos ⁡ π + j sin ⁡ π = e j π = - 1 ...

c n = - 1 4 π 1 - n 2 e j π e - j n π + n e j π e - j n π + e j π e - j n π - n e j π e - j n π - 2 →

Então, cortando...

c n = - 1 4 π 1 - n 2 - 2 e - j n π - 2 →

c n = 2 4 π 1 - n 2 e - j n π + 1 →

c n = e - j n π + 1 2 π 1 - n 2

Passo 3

Ta aí! Os nosso coeficientes. De acordo com Fourier podemos então representar f assim:

f t = ∑ n = - ∞ ∞ c n e j ω 0 n t =

∑ n = - ∞ ∞ e - j n π + 1 2 π 1 - n 2 e j ω 0 n t

Resposta

f t = ∑ n = - ∞ ∞ e - j n π + 1 2 π 1 - n 2 e j ω 0 n t

Ver Outros Exercícios desse livro