Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 76
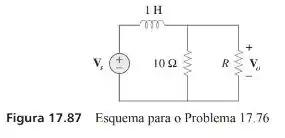
Um sinal periódico dado por para e para é aplicado ao filtro passa-altas da figura 17.87. Determine o valor de tal que o sinal de saída tenha uma potência média de pelo menos da potência média do sinal de entrada.
Passo 1
O formato de é apresentado na figura do exemplo resolvido 17.1, exceto por sua magnitude que é multiplicada por 10 nesse caso. Sendo assim, já temos o formato para cuja construção é feita no exemplo resolvido do livro. Assim, temos que será dada por
A partir dessa expressão podemos extrair algumas informações que são
Passando nosso indutor para impedância vamos ter
A impedância pra parte mais direita do circuito é dada por
Sendo assim, temos, pelo divisor de tensão, que
Dado que
Passo 2
Para a fonte de corrente temos
Dessa forma, temos que a potência vai ser dada por
Passo 3
Para o caso , vai agir como um curto circuito, então, teremos
Assim, teremos nossa potência como sendo
Lembrando que
Desejamos que a potência de saída seja de . Aqui vamos utilizar uma aproximação devido a complexidade dos termos (cada vez que eles aumentam no denominador o número como um todo vai diminuindo),sendo assim, vamos usar como uma forma de aproximação apenas o componente então teremos