Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 10
10. Usando a figura elabore um problema para ajudar outros estudantes a entenderem melhor o teorema da superposição. Note que a letra é um ganho que você pode especificar de forma a tornar o problema de fácil solução, mas seu valor não deve ser nulo.
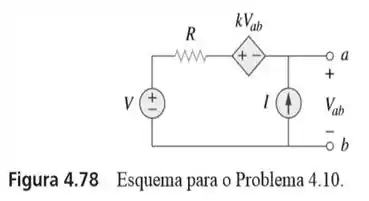
Passo 1
Olha só! Como é um problema que nós mesmos teremos que elaborar, bora redesenhar esse circuito, atribuindo valores numéricos para seus elementos.
E aqui está:
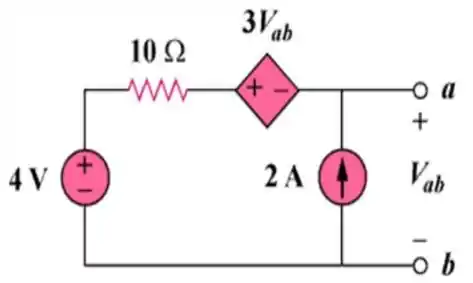
E o problema proposto é o seguinte... Usando o teorema da superposição, teremos que determinar o valor de ... Bora lá por a mão na massa, então:
No circuito que redesenhamos, há a presença de duas fontes independentes; uma fonte de tensão e uma fonte de corrente.
Logo, usando superposição, temos que a tensão é dada pela soma das contribuições de corrente das duas fontes individualmente. No caso, chamaremos de a contribuição da fonte de tensão e de a contribuição da fonte de corrente.
Passo 2
Primeiro, vamos determinar . Para isso, vamos abrir o circuito no ramo onde está a fonte de corrente.
De modo que nosso circuito passa a ter a seguinte cara:
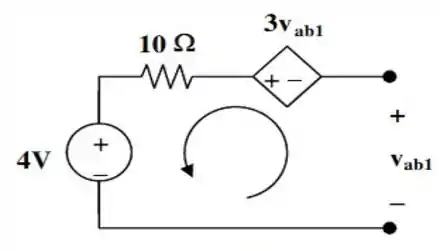
Aplicando a lei das tensões de , , podemos determinar facilmente o valor de . Desse jeito aqui...
Passo 3
Em seguida, vamos determinar . Para isso, vamos retirar a fonte de tensão, substituindo por um curto circuito e deixando apenas a fonte de corrente.
E o circuito fica desse jeito aqui:
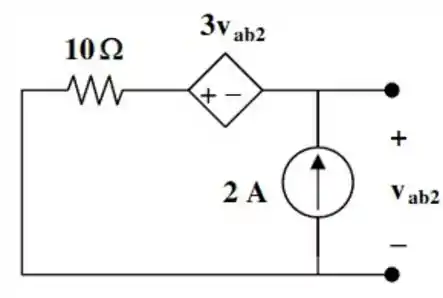
Aplicando a , assim como no anterior, podemos determinar facilmente o valor de .
Que é igual a...
Passo 4
Pra finalizar, basta somar e e e encontraremos ...