Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 3.Problemas - Ex. 50
Suponha que a fonte ideal de tensão da Figura 3.26 seja substituída por uma fonte ideal de corrente. Mostre que a Equação 3.33 ainda é válida.
Passo 1
Show de bola! Vamos começar colocando a Figura 3.26 e a Equação 3.33:
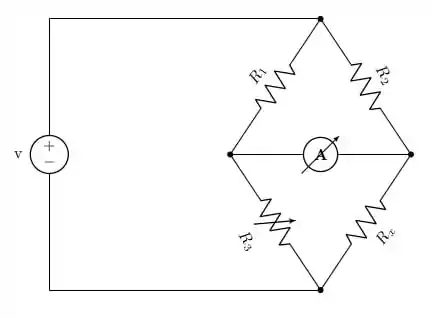
E a equação citada é
Além disso, é pedido que nós realizemos uma troca de fontes, assim, o circuito que iremos analisar é o circuito abaixo:
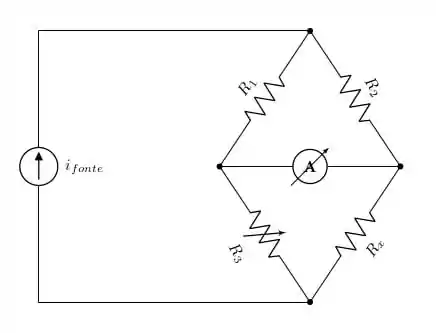
Passo 2
Para começarmos a resolver essa questão, temos que ter alguma noção da teoria. Para que a ponte de Wheatstone funcione usando a fórmula mencionada, ela tem que estar em equilíbrio. Isso significa que a corrente que passa pelo amperímetro é nula. Se ela é nula, o amperímetro pode ser retirado da ponte sem alterar o resultado. Sendo assim, a configuração seria a mostrada na figura abaixo:
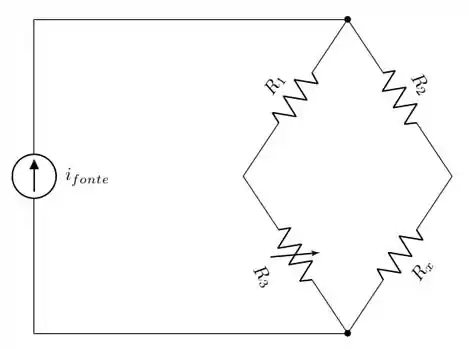
No entanto, podemos redesenhar a figura para uma topologia (nome que a gente usa para falar da maneira como o circuito está desenhado) mais conhecida e com algumas informações adicionais:
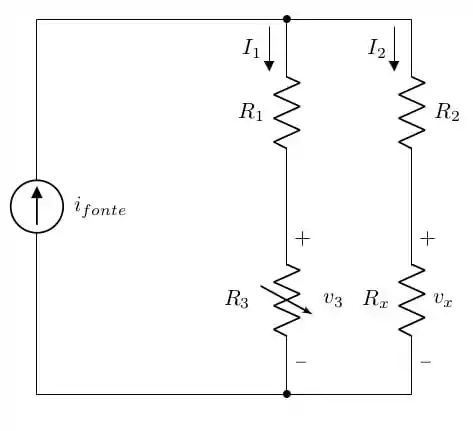
Nessa configuração, podemos usar um divisor de corrente para cada ramo e com isso vamos obter as seguintes equações:
De posse dessas equações, podemos encontrar as tensões destacadas, e :
Além disso, vamos fazer uma malha fechada fictícia que envolve os resistores e . Usando a LKT nessa malha, concluiremos que
Assim, podemos concluir que
Como os denominadores são iguais, podem ser cancelados, além do termo :
que é a Equação 3.33, como queríamos demonstrar.
Podemos perceber que esta equação teórica é bem fácil de desenvolver quando se têm em mente os princípios fundamentais do capítulo estudado. Então, vamos manter firme este entusiasmo e vamos à próxima questão!
Resposta
A demonstração