Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 2.5 - Ex. 2

Calcule R e construa um circuito equivalente com apenas uma fonte de corrente e um único resistor.

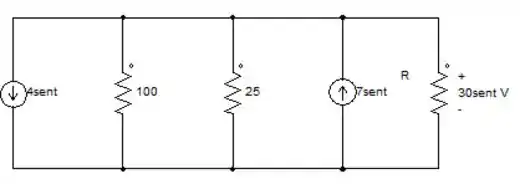
Passo 1

Para saber o i e q   basta somar as duas fontes, pois encontram-se em paralelo.

OBS: a fonte de 4 s e n   t fica negativo por estar com o sentido para baixo.

i e q =   - 4 s e n   t + 7   s e n   t  

i e q = 3   s e n   t   A

Agora vamos fazer o R equivalente dos resistores de 25Ω com 100Ω.

Eles estão em paralelo, então:

R 1 ⋅ R 2 R 1 + R 2

100 ⋅ 25 100 + 25

2500 125

R e q = 20 Ω

Passo 2

Assim fica o circuito após as contas anteriores:

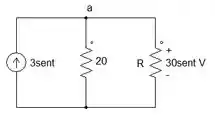
Vamos fazer lei de Ohm para saber a corrente que está passando no resistor de 20Ω.

V = R 1 ⋅ i 1

i 1 = V R 1

i 1 = 30   s e n   t 20

i 1 = 1,5   s e n   t   A

Agora, precisamos fazer LKC no nó a:

i e q = i 1 + i 2

i 2 = i e q - i 1

i 2 = 3   s e n   t   - 1,5   s e n   t

i 2 = 1,5   s e n   t   A

E, por fim, para fazemos lei de Ohm para encontrar o R .

V = R ⋅ i 2

R = V i 2

R = 30   s e n   t 1 ,   5   s e n   t

R = 20 Ω

Passo 3

Agora que descobrimos o valor de R , vamos fazer a associação de resistores entre 20 Ω e 20 Ω .

R 1 ⋅ R R 1 + R

20 ⋅ 20 20 + 20

400 40

R t o t a l = 10 Ω

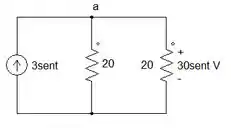
O circuito equivalente será:

Resposta

R = 20 Ω

Uma fonte de corrente i e q = 3   s e n   t   A , sentido para cima, em série com um resistor de 10 Ω

Exercícios de Livros Relacionados

Considere a interligação mostrada na Figura P2.7. a) Qual é o valor de a necessário para tornar válida essa interligação? b) Para esse valor de a, determine a potência associada à fonte de corrente. c
Se a interconexão na Figura P2.4 é válida, determine a potência total fornecida pelas fontes de tensão. Se a interconexão não é válida, explique a razão.
a) A interconexão na Figura P2.8 é válida? Explique. b) Você pode determinar a energia total relacionada ao circuito? Explique.
Se a interconexão na Figura P2.9 é válida, determine a potência total fornecida ao circuito. Se a interconexão não é válida, explique a razão.
A interconexão de fontes ideais pode resultar em uma solução indeterminada. Com isso em mente, explique por que as soluções para v1 e v2 no circuito da Figura P2.5 não são únicas.