Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 19.Problemas - Ex. 88
Use os parâmetros para obter fórmulas para para o circuito com transistor de emissor comum.
Passo 1
Vamos considerar o seguinte circuito:
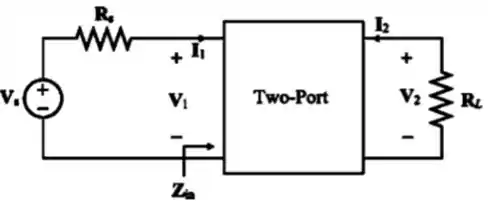
Passo 2
Os parâmetros são:
Da figura, temos a corrente que passa no resistor:
Substituindo por na equação (2):
Passo 3
Substituindo por
Além disso, temos que e .
Passo 4
A impedância interna é:
Então, substituindo por
Passo 5
O ganho da corrente é:
Substituindo por
E então,
Passo 6
O ganho da tensão é:
Substituindo por
Passo 7
Para calcularmos a impedância de saída, precisamos curto-circuitar a entrada e conectar uma fonte teste na saída:
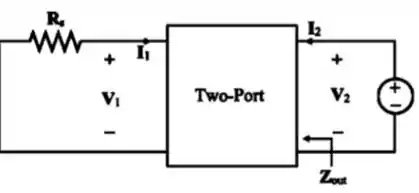
Aplicando a lei de Kirchhoff das tensões no lado esquerdo:
Substituindo por :
E substituindo por