Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 59

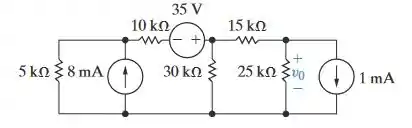
a) Use uma série de transformações de fonte para determinar a tensão v 0 no circuito da Figura P4.59.

b) Verifique sua solução usando o método das correntes de malha.

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

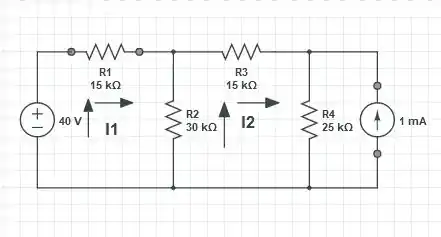
A - A fonte de corrente de 8 mA conectada em paralelo com o resistor de 5   k Ω será transformada em uma fonte de tensão de 40 V em série com o resistor de 5   k Ω . Logo, o circuito terá a seguinte configuração

Passo 2

A fonte de tensão de 75 V conectada em série com o resistor de 15k será transformada em uma fonte de corrente de 5 mA em paralelo com o resistor de 15k, e esse resistor está conectado com um de 30k, traduzindo isso tudo para conta, nós temos que

R e q = 15 × 30 15 + 30 × 10 3 = 10   k Ω

O circuito resultante é igual a

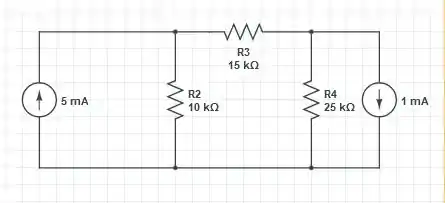
A corrente através do resistor de 25k i0 pode ser obtida realizando a divisão de corrente duas vezes, uma para a fonte de corrente de 5 mA e outra para a fonte de corrente de 1 mA,

i o 1 = 5 × 10 40 + 10 = 1   m A

E

i o 2 = - 1 × 25 25 + 25 = - 0,5   m A

Portanto,

i o = i o 1 + i o 2 = 0,5   m A

E v 0 pode ser obtido por substituição direta na Lei de Ohm,

v 0 = i o R = 0,5 × 25 = 12,5   V

Logo

v 0 = 12,5   V

Passo 3

B – Aplicando análise de malhas para o circuito mostrado, para a primeira malha

- 75 + 15 I 1 + 30 I 1 - I 2 = 0

Rearranjando, temos

45 I 1 - 30 I 2 = 75   1

Para a segunda malha, nós temos

25 I 2 - 1 + 15 I 2 + 30 I 2 - I 1 = 0  

Rearranjando

- 30 I 1 + 70 I 2 = 45   ( 2 )

Resolvendo ( 1 ) e ( 2 ) , obtemos o seguinte resultado

I 1 = 8 3 m A   e   I 2 = 1,5   m A

Com isso, v 0 é dado por

v 0 = I 2 - 1 R = 0,5 × 25 = 12,5   V

Resposta

a )   12,5   V

b )   12,5   V

Exercícios de Livros Relacionados

Dois resistores de 10K Ω são conectados em serie a uma fonte de 100V Que valor de tensão irá medir 0 voltímetro do Problema 2.41 sobre um dos resistores de 10K Ω Repita para dois resistores de 1 M Ω l
Considere a interligação mostrada na Figura P2.7. a) Qual é o valor de a necessário para tornar válida essa interligação? b) Para esse valor de a, determine a potência associada à fonte de corrente. c
Se a interconexão na Figura P2.4 é válida, determine a potência total fornecida pelas fontes de tensão. Se a interconexão não é válida, explique a razão.
a) A interconexão na Figura P2.8 é válida? Explique. b) Você pode determinar a energia total relacionada ao circuito? Explique.
Se a interconexão na Figura P2.9 é válida, determine a potência total fornecida ao circuito. Se a interconexão não é válida, explique a razão.