Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 4.Problemas - Ex. 8
8-
Um resistor de 50 V é ligado em série com a fonte de corrente de 40 mA no circuito da Figura P4.6.
a) Determine Vo.
b) Determine a potência fornecida pela fonte de corrente de 40 mA.
c) Determine a potência fornecida pela fonte de tensão de 24 V.
d) Verifique que a potência total fornecida é igual à potência total dissipada.
e) Qual será o efeito de qualquer resistência finita ligada em série com a fonte de corrente de 40 mA sobre o valor de Vo?
Passo 1
Então, vamos enfrentar essa fera... brincadeira rsrs. Essa questão é suave na nave, basta que a gente pense um pouquinho, vamos nessa?!
a)
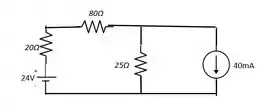
Fig. P4.6.
Primeiro a gente precisa achar Vo, que está em cima do resistor de 25Ohms. Para fazer isso é necessário que utilizemos o método das tensões de nó, onde:
;
Vo = 4 V
Passo 2
b) Se Vx é igual a tensão na fonte de 40 mA , então:
Vx = Vo − (50)*(0.04) = 2 V
Com essa tensão, a gente pode calcular a potência, vamos lá:
p40mA = (2)*(0.04) = 80 mW
Então p40mA (forneceu) = −80 mW
Passo 3
c) Se ig é igual a corrente no terminal positivo da fonte de 24v, então:
ig = (4 − 24)/100 = −0.2 A
p24V = (−0.2)*(24) = −4800 mW
Então p24V (forneceu) = 4800 mW
Passo 4
d) Xpdis =
= 4800 mW
Passo 5
Ufffaaaa, finalmente a ultima letra rsrsrs... Vamos destruir logoo!
e) Então, analisando a gente percebe que Vo é independente de qualquer resistência finita em série conectada com a fonte de corrente de 40m.
Resposta
Ei, a resposta está no passo a passo :)