Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Johnson, D. E., Hilburn, J. L., Johnson, J. R. - Fundamentos de Análise de Circuitos Elétricos, PHB- Ed: 4º - Capítulo 8.9 - Ex. 3

Use a superposição para calcular i para t > 0 . Assuma que o circuito está na condição de regime permanente em t = 0 - .

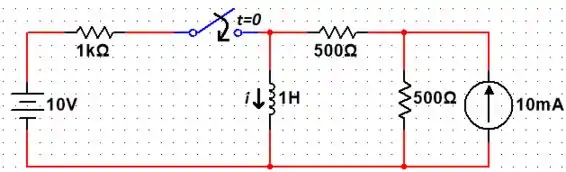
Passo 1

Eaee meu/minha consagradx!!! Beleza?? Se liga aqui!!

Como a questão pede pelo teorema da superposição, vamos primeiro fazer o circuito só com a fonte de tensão e depois a gente faz só com a fonte de corrente. Beleza?

Passo 2

Utilizando só a fonte de tensão, a gente considera a fonte de corrente como um circuito aberto e já somamos aqueles dois resistores em série de tal forma que o circuito fica da seguinte forma:

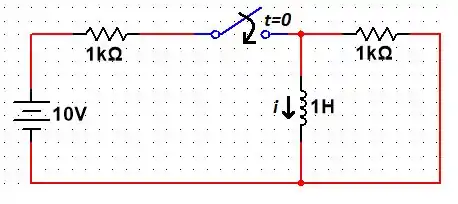
Agora, vamos calcular o equivalente de Thévenin nos terminais do indutor (substituindo a fonte de tensão por um curto circuito):

R T H = 1 k Ω | | 1 k Ω ∴ R T H = 500 Ω  

E a tensão de Thévenin é a queda de tensão em um resistor de 1 k Ω . E, como as resistências são iguais no circuito acima, significa dizer que:

V T H = 10 2 = 5 V

Além disso, temos que a constante de tempo τ é dada por:

τ = L R T H = 1 500 s

Passo 3

Quando a chave é fechada, a corrente i no indutor é dada por:

i = V T H R T H ( 1 - e - t τ )

Assim, substituindo os valores, temos:

i = 5 500 1 - e - 500 t ∴

i = 1 1 00 1 - e - 500 t   A

Passo 4

Agora, tratando a fonte de tensão como um curto circuito, temos:

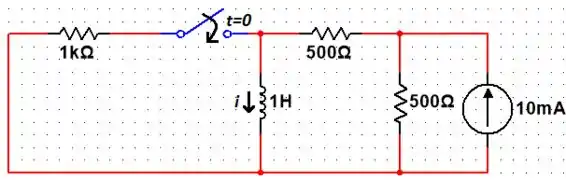
Fazendo a mesma coisa que fizemos anteriormente, devemos encontrar o equivalente de Thévenin nos terminais do indutor. Então, tratando a fonte de corrente como o circuito aberto podemos encontrar a resistência de Thévenin R T H :

R T H = 1 k Ω | | 500 Ω + 500 Ω ∴ R T H = 500 Ω

Para determinarmos a tensão de Thévenin V T H , é possível percebermos que será a mesma tensão encontrada no resistor de 1 k Ω pois este está em paralelo com o indutor. Dessa forma, podemos utilizar o divisor de corrente no circuito abaixo:

i ' = 10 × 10 - 3 500 1500 + 500 = 1 400 A

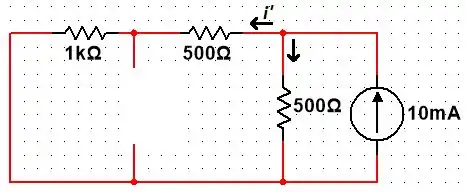
Assim, a tensão de Thévenin é dada por:

V T H = 1 k Ω × 1 400 ∴ V T H = 2.5 V

Além disso, temos que a constante de tempo τ é dada por:

τ = L R T H = 1 500 s

Passo 5

Quando a chave é fechada, a corrente i no indutor é dada por:

i = V T H R T H ( 1 - e - t τ )

Assim, substituindo os valores, temos:

i = 2 . 5 500 1 - e - 500 t ∴

i = 1 2 00 1 - e - 500 t   A

Passo 6

Agora é só somar as duas correntes que encontramos por conta do princípio da superposição haha. Assim, temos:

i = 1 100 1 - e - 500 t + 1 200 1 - e - 500 t ∴

i = 3 200 1 - e - 500 t

Resposta

i = 3 200 1 - e - 500 t

Exercícios de Livros Relacionados

O pulso na figura 7.116a pode ser expressa em termos de funções de singularidade como: a2 u t + 2 u t - 1V b2 u t - 2 u t - 1V c2 u t - 4 u t - 1V d2 u t + 4 u t - 1V
Se v s mudar de 2 V para 4 V em t = 0 , podemos expressar v s como: aδ tV b2 u tV c2 u - t + 4 u tV d2 + 2 u tV e4 u t - 2V
A forma de onda de tensão mostrada na Figura P7.82 (a) é aplicada ao circuito da Figura P7.82(b). A corrente inicial no indutor é igual a zero.Calcule v 0 ( t ) .Faça um gráfico de v 0 t em função de
A fonte de corrente no circuito da Figura P7.81 (a) gera o pulso de corrente mostrado na Figura P7.81(b). Não há nenhuma energia armazenada em t=0.Deduza as expressões numéricas de v 0 ( t ) para os i
Calcule i para t0 , se v g = 12 u t V ,