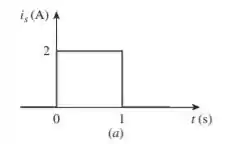
O pulso na figura 7.116a pode ser expressa em termos de funções de singularidade como:

Como todas as alternativas dadas estão em função da função degrau unitário alguns comentários são relevantes sobre essa função:

• Dado o tempo que zera o que está dentro do argumento de indica o valor onde a função começa a ter seu valor igual a 1 e assim segue até o infinito, exceto no caso em que tenha um outro degrau subtraindo;
• Para nosso, caso como temos percebemos que o valor de que zera o argumento é . Dessa forma, temos que a alternativa que melhor representa o pulso mostrado na imagem é o da alternativa que traz um pulso que vem do valor 2 (por conta do escalar multiplicando) e é zerado abruptamente em que é o degrau também multiplicado pelo escalar 2.