Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 31

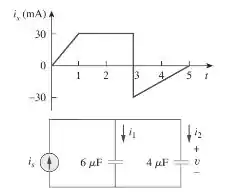
Se V(0) = 0, determine V(t), i1 (t) e i2(t) no circuito da figura abaixo.

Passo 1

Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para calcular a tensão em cima do capacitor e as correntes de cada ramo. Parece muita coisa, mas é tranquilo. Partiu??

Passo 2

Ok, agora o nosso problema vai ser relembrar qual a relação que nos dá a corrente de um capacitor. Lembrou?? Não?! Dá um pulo lá em Física 3 rapidinho que eu te espero... Já voltou?? Então, me conta aii qual é a fórmula... Acertou, misêrávi!!

i = C d v d t

Mas, como queremos descobrir a tensão, vamos transformar para a notação integral.

v = 1 C   ∫ i   d t + v ( 0 )

Como ele nos deu a relação para a corrente e o valor de C, agora é só jogar os valores ali.

Passo 3

Pronto!! Agora é só jogar daqui pra lá e de lá pra cá!!

v 1 = 10 - 3 10 x   10 - 6   ∫ 30 t   d t + 0

v 1 = 1,5   t 2 k V

V o 1 = 1,5   k V

v 2 = 10 - 3 10   x   10 - 6   ∫ 20   d t + 1,5

v 2 = 3 t - 1,5 k V  

v 3 = 10 - 3 10   x   10 - 6   ∫ ( 15 t - 5 )   d t + 7,5

v 3 = 0,75 t ² - 7,5 t + 23,25 k V

Como já achamos as tensões em todos os trechos do circuito, vamos achar as correntes pela nossa formulinha lá do início. Nosso gráfico está dividido entre as regiões de 0 a 1, 1 a 3 e 3 a 5. Com isso, vamos botar os extremos e encontrar as relações.

i 1 =   18 t   m A ,   0 < t < 1 18   m A ,   1 < t < 3 9 t - 45 m A ,   3 < t < 5

i 2 =   12 t   m A ,   0 < t < 1 12   m A ,   1 < t < 3 6 t - 30 m A ,   3 < t < 5

Resposta

v 1 = 1,5   t 2 k V

v 2 = 3 t - 1,5 k V  

v 3 = 0,75 t ² - 7,5 t + 23,25 k V

i 1 =   18 t   m A ,   0 < t < 1 18   m A ,   1 < t < 3 9 t - 45 m A ,   3 < t < 5

i 2 =   12 t   m A ,   0 < t < 1 12   m A ,   1 < t < 3 6 t - 30 m A ,   3 < t < 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Indutores em paralelo podem ser associados da mesma forma que resistores em paralelo.VerdadeiroFalso
Se a corrente através de um indutor e 10 mH aumenta de zero a 2 A, qual é a quantidade de energia armazenada no indutor??40 mJ20 mJ 10 mJ5 mJ
Um capacitor de 4mF apresenta a seguinte tensão em seus terminais. v =50V ,t ≤ 0 Ae - 100 t + B e - 600 t ,t ≥ 0 Se o capacitor tiver uma corrente inicial de 2A, determine a energia armazenada no capa
Em t=0, a tensão em um capacitor de 25 mF é 10 V. Calcule a tensão do capacitor para t0 quando a corrente 5t mA passa através dele.
Um capacitor de 4mF apresenta a seguinte tensão em seus terminais. v =50V ,t ≤ 0 Ae - 100 t + B e - 600 t ,t ≥ 0 Se o capacitor tiver uma corrente inicial de 2A, determine as constantes A e B.