Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 10
10. Foram efetuados experimentos para determinar coeficientes de transferência de calor locais para o escoamento perpendicular a uma longa barra isotérmica de seção transversal retangular. A barra tem largura c, paralela ao escoamento, e altura d, normal ao escoamento. Para números de Reynolds na faixa de 104 ≤ Red ≤ 5 × 104, os números de Nusselt médios nas superfícies são bem correlacionados por uma expressão na forma
Os valores de C e m para a face frontal, faces laterais e face posterior da barra retangular foram determinados e são mostrados a seguir:
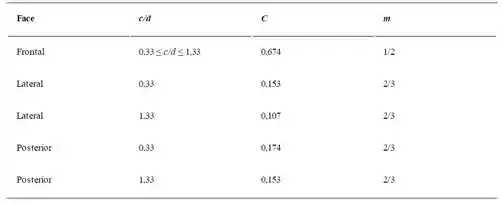
Determine o valor do coeficiente de transferência de calor médio para a superfície exposta total (isto é, média no total das quatro faces) em uma barra retangular com c = 40 mm e d = 30 mm. A barra está exposta ao escoamento cruzado de ar com V = 10 m/s e T∞ = 300 K. Forneça uma explicação plausível para os valores relativos dos coeficientes de transferência de calor
médios nas faces frontal, laterais e posterior.
Passo 1
Primeiramente, devemos obter as seguintes propriedades na tabela “Propriedades termo-físicas do ar à pressão atmosférica” e
A viscosidade cinemática é
O número Prandtl é
A condutividade térmica é
Calcule o número de Reynolds.
Face frontal:
Calcular o número de Nusselt para a face frontal
Portanto, o coeficiente de transferência de calor para a face frontal é .
Passo 2
Face lateral:
Calcular o número de Nusselt para a face frontal
Portanto, o coeficiente de transferência de calor para a face frontal é
Passo 3
Face traseira:
Calcular o número de Nusselt para a face frontal
Portanto, o coeficiente de transferência de calor para a face frontal é