Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 12

12. Ar com uma temperatura na corrente livre de T∞ = 20°C, escoa paralelamente sobre uma placa plana de comprimento L = 5 m e temperatura Ts = 90°C. Entretanto, obstáculos colocados no escoamento intensificam a mistura com o aumento da distância x da aresta frontal e a variação espacial das temperaturas medidas no interior da camada-limite é correlacionada por uma expressão da forma T(°C) = 20 + 70 exp(−600xy), com x e y em metros.

Determine e represente graficamente a maneira pela qual o coeficiente convectivo local h varia com x. Calcule o coeficiente convectivo médio para a placa.

Passo 1

Antes de mais nada devemos aplicar o balanço energético ao sistema.

h T s - T ∞ = - k ∂ T ∂ y y = 0

Substituindo a expressão de T:

h T s - T ∞ = - k ∂ ( 20 + 70 e - 600 x y ∂ y y = 0

h T s - T ∞ = - k 70 × - 600 x e - 600 x y

h T s - T ∞ = - k 70 × - 600 x e - 0

h = k ( 70 × 600 x ) T s - T ∞

h = 0,0284 ( 70 × 600 x ) 90 - 20

h = 17 x     ( 1 )

Cálculo da amostra:

Para x = 1   , a equação (1) reduz da seguinte forma:

h = 17 x

= 17 W m 2 . K

Da mesma forma, tabule os valores de  h   para vários valores de  x .

Traçar o gráfico de  h versus  x .

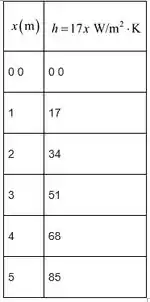
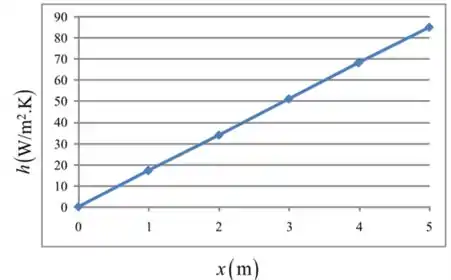
Passo 2

Calcule o coeficiente médio de transferência de calor por meio de:

h - = 1 L ∫ 0 5 h d x

Substitua  17 x   por  h .

h - = 1 L ∫ 0 5 ( 17 x ) d x

= 17 L x 2 2 0 5

h - = 17 5 5 2 - 0 2 2

= 42,5 W m 2 . K

Portanto, o coeficiente médio de transferência de calor é  42,5 W m 2 . K .

Resposta

h = 17 x

h - = 42,5 W m 2 . K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

19. Um ventilador que pode fornecer velocidades de ar de até 50 m/s deve ser usado em um túnel de vento de baixa velocidade com ar atmosférico a 25°C. Se alguém desejar usar o túnel de vento para estu
9. Um jato circular de gases quentes a T∞ encontra-se direcionado normalmente a uma placa circular, que tem raio r0 e é mantida a uma temperatura uniforme Ts. O escoamento do gás sobre a placa é axiss
8. Na convecção natural em regime laminar em uma superfície vertical aquecida, o coeficiente convectivo local pode ser representado por hx =Cx−1/4, sendo hx o coeficiente a uma distância x da aresta f
13. A taxa de transferência de calor, por unidade de largura (normal à página), em uma seção longitudinal, x2 – x1, pode ser representada por = 12 (x2 – x1)(Ts – T∞), sendo 12 o coeficiente médio na s