Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 6.Problemas - Ex. 17

17. Seja o disco em rotação do Problema 6.16. Uma placa estacionária, em forma de disco, é posicionada um pouco acima do disco em rotação, formando um espaço de espessura g. A placa estacionária e o ar ambiente estão a T∞ =20°C. Se o escoamento for laminar e a razão entre a espessura do espaço entre discos e o raio dos discos, G = g/re, for pequena, a distribuição de números de Nusselt locais tem a forma

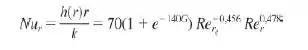
com Rer = Ωr2/v [Pelle, J. e S. Harmand, Exp. Thermal Fluid Science, 31, 165, 2007]. Determine o valor do número de Nusselt médio, = D / k, sendo D = 2re. Sendo a temperatura do disco em rotação igual a Ts = 50°C, qual é o fluxo térmico total saindo da superfície superior do disco para g = 1mm, Ω = 150 rad/s? Qual é a potência elétrica total requerida? O que você pode falar sobre a natureza do escoamento entre os discos?

Passo 1

Escreva a equação no número de Nusselt da seguinte maneira:

N u r = h r r k

= 70 1 + e - 140 G R e r 0 - 0,456 R e r 0,478

Quando, R e r = Ω r 2 v

Calcule o coeficiente de transferência de calor local da seguinte maneira:

h r = k 70 1 + e - 140 G Ω r 0 2 v - 0,456 Ω r 0,478

Calcule o coeficiente médio de transferência de calor usando a seguinte equação:

h - = 2 π k π r 0 2 70 1 + e - 140 G Ω r 0 2 v - 0,456 Ω v 0,478 ∫ r × r - 0,044 d A s

= 1,022 k r 0 2 70 1 + e - 140 G Ω r 0 2 v - 0,456 Ω r 0,478 r 0 1,956

Calcule a temperatura média.

T - = T s + T ∞ 2

= 50 + 20 2

35 ° C + 273 = 308   K

Obtenha as propriedades da tabela "Propriedades termo-físicas dos gases" à pressão atmosférica e temperatura média  308 K .

A condutividade térmica do ar é k = 0,0269 W m . K  

Viscosidade cinemática do ar é v = 16,69 × 10 - 6 m 2 s  .

h - = 1,022 × 0,0269 0,100 2 70 1 + e - 140 × 0,01 150 × 0,100 2 16,69 × 10 - 6 - 0,456 150 16,69 × 10 - 6 0,478 0,100 1,956

= 30,8 W m 2 . K

Determine o número médio de Nusselt usando a seguinte equação:

N u D = h - D k

N u D = 30,8 × 0,2 0,0269

= 229

Portanto, o valor do número médio de Nusselt é  229 .

Passo 2

Calcule o fluxo de calor da superfície superior do disco rotativo usando a equação: 

q ' ' = h - ( T s - T d )

= 30,8 ( 50 - 20 )

= 924 W m 2

Portanto, o fluxo total de calor da superfície superior do disco é  924 W m 2 .

Agora, calcule o requisito total de energia elétrica.

P = q ' ' . A s

= q ' ' . π r 0 2

P = 924 × π 0,100 2

= 29   W

Portanto, o requisito total de energia elétrica é  29   W .

Observe que, se apenas ocorresse condução entre os dois discos, calcule o fluxo de calor da seguinte maneira:

q ' ' = k g ( T s - T d )

= 0,0269 0,001 × 50 - 20

= 807 W m 2

Assim, é visto que o fluxo de calor de condução é em certa medida menor que o fluxo de calor com rotação. Indica uma pequena convecção na direção da folga cruzada e também prova que a transferência de calor entre os discos está sujeita principalmente à condução.

Velocidades muito baixas na direção da folga cruzada descrevem o fluxo laminar que ocorre nos discos.

Resposta

N u D = 229

P = 29   W

q ' ' = 807 W m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Obtenha uma expressão para a espessura do filme líquido, considerando a igualdade entre as teorias de penetração e do filme;
Obtenha uma expressão para k m semelhantes a equação (7.11), considerando que a placa-plana esteja inclinada, em relação a um plano horizontal, com inclinação igual a α .
Considerando que o soluto esteja distribuído nas fases gasosas e líquida e sabendo que a interface não oferece resistência ao fluxo do soluto, obtenha as seguintes relações como função das respectivas
Desenvolva um programa numérico e resolva a equação ( 7.127 )
Refaça o exercício 3, considerando o etanol como fluido de trabalho. Compare os resultados obtidos com o exercício 3 e os analise.