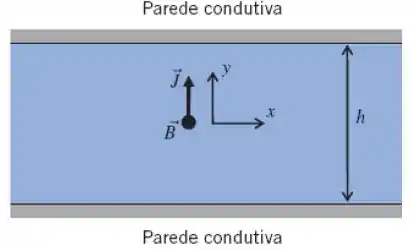
5.95 Considere um microcanal plano com largua h, conforme mostrado (o microcanal realmente é muito longo na direação x e aberto em ambas extremidades). Um sistema de coordenadas Cartesianas com a sua orgiem posicionada no centro do microcanal é usado neste estudo. O microcanal é preenchido com uma solução de baixa conditividade elétrica. Quando uma corrente elétrica é aplicada através das duas parades condutivas, a densidade de corrente elétrica, , transmitida através da solução é paralela ao eixo y. Todo este dispositivo é colocado em um campo magnético constante, , que está apontando para fora do plano xy (a direação z), como mostrado. A interação entre a densidade de corrente elétrica e o campo magnético induz uma força de Lorentz de densidade . Considere que a solução condutiva é incompressível, e uma vez que o volume de amostragem é muito pequeno em aplicações em um laboratório integrado em um chip a força de campo gravitacional pode ser desprezada. Em regime permanente, o escoamento acionado pela força de Lorentz é descrito pela equação da continuidade (Eq. 5.1a) e pelas equações de Navier-Stokes (Eqs. 5.27), exceto as componentes x, u e z, das equações de Navier-Stokes que possuem componentes da força de Lorentz extra no lado direito. Considerando que o escoamento é completamente desenvolvido e que o campo de velocidade é uma função somente de y, determine as três componentes da velocidade.

Simplificando as equações com :

Considerando o gradiente de pressão igual a zero, a equação de quantidade de movimento se reduz a:

Separando as variáveis e integrando em relação a y:

De novo:

Aplicando as condições de contorno:

Em :

Em :

Resolvendo o sisteminha:

A velocidade, então: