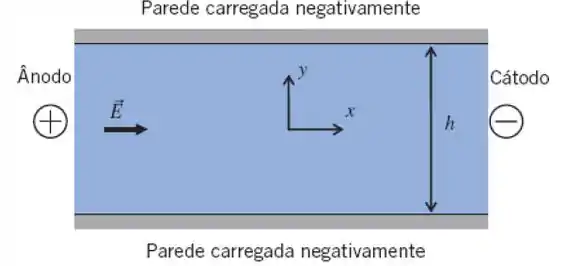
5.97 Escoamento eletroosmótico (EOF) é o movimento de líquido induzido por um campo elétrico aplicado através de um tubo capilar ou microcanal carregado com energia elétrica. Considere que a parede do canal está negativamente carregada, uma camada final chamada camada dupla elétrica (EDL na sigla em inglês) se forma na vizinhança da parede do canal na qual o número de íons positivos é muito maior do que o número de íons negativos. Os íons carregados negativamente na EDL arrastam então juntamente consigo a solução eletrolítica e causam o escoamento do fluido em direção ao cátodo. A espessura da EDL tem valor típico da ordem de 10 nm. Quando as dimensões do canal são muito maiores do que a espessura da EDL, existirá uma velocidade de deslizamento, , sobre a parede do canal, em que ε é a permissividade do fluido, ζ é o potencial elétrico da superfície negativa, é a intensidade do campo elétrico, e μ é a viscosidade dinâmica do fluido. Considere um microcanal formado por duas placas paralelas. As paredes do canal possuem um potencial elétrico de superfície negativo de ζ. O microcanal é preenchido com uma solução eletrolítica, e as extremidades do microcanal são submetidas a uma diferença de potencial elétrico que dá origem a um campo

elétrico uniforme de magnitude E ao longo da direção x. O gradiente de pressão no canal é zero. Deduza a velocidade do escoamento eletroosmótico, em regime permanente, completamente desenvolvido. Compare o perfil de velocidade do EOF com aquele do

escoamento devido a um diferencial de pressão. Calcule a velocidade do EOF usando ε = 7,08 × 10–10 CV–1m–1, ζ = 0,1 V, μ = 10–3 Pa ·

s e E = 1000 V/m.

Passo 1

Passo 2

Passo 3

Resposta