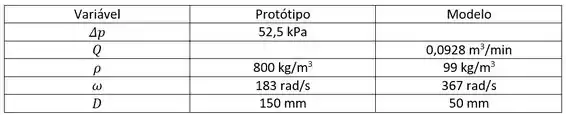
O aumento de pressão, , de um líquido escoando em regime permanente através de uma bomba centrífuga depende do diâmetro da bomba, , da velocidade angular do rotor, , da vazão volumétrica, , e da massa específica, . A tabela fornece dados para o protótipo e para um modelo de bomba geometricamente semelhante. Para condições correspondentes à semelhança dinâmica entre as bombas modelo e protótipo, calcule os valores que faltam na tabela.

Definindo os parâmetros dimensionais conforme apresentados no enunciado: aumento de pressão (), velocidade angular (), vazão (), diâmetro da bomba () e massa específica ().

Logo o número de parâmetros dimensionais é:

Escolhendo as dimensões primárias:

-

-

-

-

-

Logo, as dimensões primárias são , e , ou seja:

Os parâmetros repentes serão .

Neste problema como parâmetros repetentes serão escolhidos , e , os quais representam as características dinâmica, cinética e geométrica, respectivamente.

Número de parâmetros adimensionais ():

Os adimensionais a serem obtidos podem ser escritos como:

-

Montando o sistema linear:

Resolvendo o sistema:

Logo:

De forma que vale:

-

Montando o sistema linear:

Resolvendo o sistema:

Logo:

De forma que vale:

Na Tabela do enunciado não são conhecidos a vazão do protótipo e o aumento de pressão do modelo, então serão utilizados os adimensionais obtidos:

- Vazão do protótipo

A partir do adimensional , garantido semelhança geométrica e cinética, a semelhança dinâmica fornecerá:

Logo, a vazão do protótipo pode ser escrita como:

Utilizando os valores numéricos conhecidos:

A vazão do protótipo vale:

- Aumento de pressão do modelo

A partir do adimensional , garantido semelhança geométrica e cinética, a semelhança dinâmica fornecerá:

Logo, o aumento de pressão do modelo pode ser escrita como:

Utilizando os valores numéricos conhecidos:

O aumento de pressão do modelo vale: