Água entra em um duto retangular liso de de comprimento com e . A temperatura da superfície é mantida constante, e a água entra no tubo a com vazão de . Determine a temperatura de superfície do tubo necessária para aquecer a água à temperatura de saída desejada de .
Passo 1
Dados fornecidos:
Vazão mássica:
Temperatura média da água na entrada:
Temperatura média da água na saída:
Comprimento do tubo:
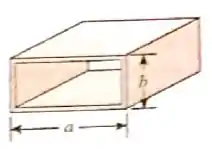
Largura do tubo:
Altura do tubo:
Passo 2
Para resolver a questão, começamos calculando a temperatura média da água com a seguinte relação:
Aqui, é a temperatura média de entrada e é a temperatura média de saída da água. Substituindo os termos pelos dados fornecidos no enunciado, temos:
Com o valor da temperatura média, podemos obter as seguintes propriedades da água em a na Tab. A-9.
Condutividade térmica:
Viscosidade dinâmica:
Calor específico:
Densidade da água:
Número e Prandtl:
Passo 3
Agora, vamos calculando o diâmetro hidráulico do tubo retangular. Assim temos:
Aqui, é o diâmetro hidráulico, é a área da seção transversal do duto e é o perímetro do duto. Substituindo os termos da equação pelos dados fornecidos, temos:
Também temos que calcular a veleidade média. Podemos fazer isso com a seguinte relação:
Aqui, é o área da seção transversal, é a densidade da água e é a taxa de fluxo de massa.
Passo 4
Com a velocidade média, podemos calcular o número de Reynolds usando a seguinte relação:
Substituindo a velocidade média, temos:
Substituindo os termos pelos dados fornecidos no enunciado, temos:
O valor calculado do número de Reynolds é maior que , portanto, é um fluxo turbulento. Temos que o comprimento da entrada hidrodinâmica e entrada térmica para o fluxo turbulento é:
Como o comprimento de entrada é menor que o comprimento especificado, o fluxo é um fluxo turbulento totalmente desenvolvido.
Passo 5
Podemos escrever a correlação do número Nusselt para um fluxo turbulento totalmente desenvolvido com superfícies lisas pela equação de Dittus-Boelter. Assim temos:
Substituindo os termos da relação pelos dados fornecidos e calculados, temos:
Com o número de Nusselt, podemos calcular o coeficiente de transferência de calor por convecção da seguinte maneira:
Aqui é a condutividade térmica. Substituindo os termos pelos dados encontrados anteriormente, temos:
Passo 6
Podemos calcular a temperatura da superfície tubo usando a seguinte relação:
Aqui é a temperatura do fluxo de entrada, é a temperatura da superfície do tubo, é a temperatura do fluxo de saída, é a área da superfície, o coeficiente de transferência de calor e é a vazão mássica da água. Temos que .
Substituindo os termos pelos dados encontrados anteriormente e fornecidos no enunciado, temos:
Portanto, a temperatura da superfície do tubo é .