Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 37

Uma aleta circular k = 240 W m ∙ K de seção transversal uniforme, com diâmetro de 10   m m e comprimento de 50   m m , é fixada a uma parede com temperatura de superfície de 350 ° C . A ponta da aleta tem temperatura de 200 ° C , exposta à condição do ar ambiente de 25 ° C e com coeficiente de transferência de calor por convecção de 250 W m 2 ∙ K . Pressupondo uma transferência de calor permanente unidimensional ao longo da aleta e um espaçamento nodal uniforme de 10   m m , ( a ) obtenha as equações de diferença finita para determinar as temperaturas nodais usando a abordagem do balanço de energia, e ( b ) determine as temperaturas nodais ao longo da aleta, resolvendo as equações, e compare os resultados com a solução analítica.

Passo 1

Primeiramente vamos separar os dados do enunciado aqui:

∆ x = 10   m m ; k = 240 W m ∙ K ; T ∞ = 25 ° C ,   T 0 = 350 ° C ,   h = 250 W m 2 ∙ K ; D = 10   m m ; L = 50   m m  

Agora podemos calcular o número de nós para o nosso problema.

M = L ∆ x + 1 = 50   m m 10   m m + 1 = 6

Muito bem!! Feito isso note que nosso nó final e também referente a ponta da aleta será o nó 5. Do enunciado a ponta da aleta tem temperatura especificada de 200 ° C . Representando o exercício:

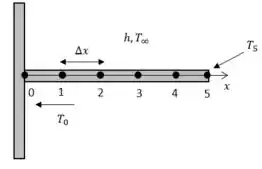
Bom, a partir da representação podemos usar nossa equação geral de diferenças finitas para se obter uma expressão para os nós interiores 1, 2, 3 e 4.

k A T m - 1 - T m ∆ x + k A T m + 1 - T m ∆ x + h p ∆ x T ∞ - T m = 0

T m - 1 - 2 T m + T m + 1 + h p ∆ x 2 k A T ∞ - T m = 0

Passo 2

Podemos usar nossa equação geral nos nós.

Para o N ó   1 :

T 0 - 2 T 1 + T 2 + h p ∆ x 2 k A T ∞ - T 1 = 0

Para o N ó   2 :

T 1 - 2 T 2 + T 3 + h p ∆ x 2 k A T ∞ - T 2 = 0

Para o N ó   3 :

T 2 - 2 T 3 + T 4 + h p ∆ x 2 k A T ∞ - T 3 = 0

Para o N ó   4 :

T 3 - 2 T 4 + T 5 + h p ∆ x 2 k A T ∞ - T 4 = 0

Note que...

p ∆ x 2 k A = 4 h ∆ x 2 k D = 4 250 W m 2 ∙ K 0,01   m 2 240 W m ∙ K 0,01   m = 0.04167

Passo 3

Pessoal agora temos as equações para cada ponto nodal, podemos resolve-las simultaneamente através de um solver...

Obtendo as seguintes temperaturas:

T 1 = 299,9 ° C

T 2 = 261,3 ° C

T 3 = 232,5 ° C

T 4 = 212,3 ° C

Passo 4

Para podermos obtermos uma solução analítica, podemos utilizar uma equação que representa a variação de temperatura ao longo da aleta.

Porém, atenção...existe mais de uma equação para isso, mas o nosso exercício aqui se trata de uma aleta com temperatura especificada na ponta!! E essa é a equação que nos dá a representação:

T x - T ∞ T b - T ∞ = T L - T ∞ T b - T ∞ senh ⁡ m x + senh ⁡ m ( L - x ) senh ⁡ m L

Muito bem!! Agora só resolvermos essa equação para cada nó, levando em conta o espaçamento entre eles.

Passo 5

Eu fiz uma tabela para gente comparar os resultados junto à um gráfico:

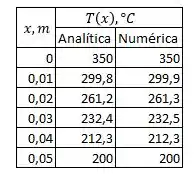
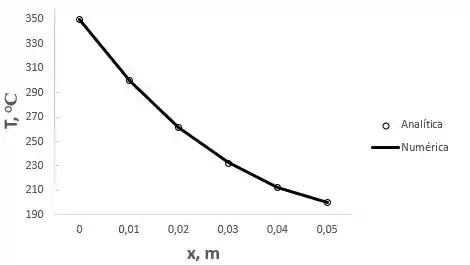
A partir do gráfico podemos concluir que ambos os resultados são bem próximos, ou seja, com pouca taxa de erro.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro