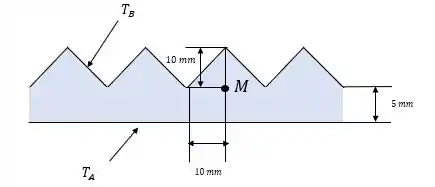
A parede do trocador de calor separa a água quente a de água fria a . Para aumentar a área de transferência de calor, ranhuras bidimensionais são usinadas no lado frio da parede, como mostrado na Fig. P5–49. Essa geometria causa tensões térmicas não uniformes, o que pode tornar crítico o aparecimento de rachaduras ao longo da linha entre duas ranhuras. Para prever a tensão térmica, o campo de temperatura no interior da parede deve ser determinado. Os coeficientes de convecção são suficientemente elevados de modo que a temperatura superficial é igual à dá água em cada lado da parede.

( Identifique a menor seção da parede que pode ser analisada a fim de encontrar o campo de temperatura em toda parede.

Para o domínio encontrado na parte , construa a malha bidimensional com e escreva a matriz de equações (os elementos das matrizes e devem ser números). Não resolva para .

Um termopar montado no ponto mede Determine as outras temperaturas desconhecidas na malha definida na parte .

Logo, nosso domínio pode ser esboçado como:

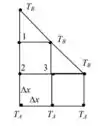
Onde nas extremidades indicadas temos as seguintes temperaturas, e .

Com isso podemos esboçar as equações de diferenças finitas para cada nó. Considerando as quatro direções. Sendo eles:

:

:

:

Agora que possuímos as equações para cada nó, podemos criar nossa matriz, certo?

Logo ela ficará assim...

Usando nossas equações encontradas anteriormente temos que .

Agora basta substituímos nas outras equações para encontrar e ...