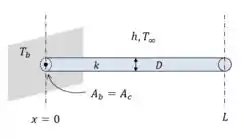
Uma aleta circular de seção transversal uniforme, com diâmetro de e comprimento de , é fixada a uma parede com temperatura de superfície de . A aleta é feita de material com condutividade térmica de , exposta ao ar ambiente na condição de e com coeficiente de transferência de calor por convecção de . Suponha uma transferência de calor constante unidimensional ao longo da aleta e um espaçamento nodal uniforme com e para determinar as temperaturas nodais obtenha as equações de diferença finita usando a abordagem do balanço de energia, determine as temperaturas nodais ao longo da aleta resolvendo as equações e compare os resultados com a solução analítica, calcule a taxa de transferência de calor e compare o resultado com a solução analítica.
Passo 1
Bora lá pessoal, como primeiro passo nos temos que extrair os dados do enunciado, eu separei aqui pra você, olha só:
Beleza! Agora precisamos encontrar o número de nós na direção que a nossa aleta terá, basta usarmos essa equação:
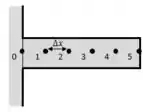
Para ficar mais visível, podemos planificar nossa aleta e acrescentar os nós, onde o nó 0 equivale a :
Passo 2
Agora precisamos expressar a formulação para diferenças finitas para os nós 1, 2, 3 e 4, a equação geral e dada por...
Vamos diminuir essa equação enorme? Basta dividirmos tudo por , ela fica assim:
Onde,
Note que o nó 5 se encontra na extremidade da aleta, logo sua equação ficara um pouco diferente, mas fica tranquilo...só precisamos considerar a convecção que se da na ponta da aleta , logo:
Onde,
Passo 3
Muito bem! Agora vamos equacionar os pontos e assim responder a letra ...
Para respondermos a letra precisamos resolver as equações acima...
Mas essas equações são enormes não é mesmo? Com um software de resolução de sistemas lineares podemos chegar nas seguintes temperaturas:
Note que o exercício se trata de uma aleta, logo precisamos de uma equação que nos de a variação de temperatura ao longo da aleta, porém temos que tomar cuidado, pois se trata de uma aleta convectiva que significa que sua ponta não é isolada, logo a equação que queremos é essa aqui:
Com essa equação podemos calcular a temperatura em cada ponto ao longo da aleta e comparar com os valores numéricos:
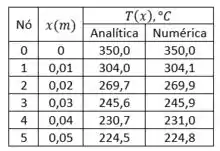
A diferença entre os dois resultados é decorrente da natureza aproximada da análise numérica, porém os valores deram próximos não? A pequena discrepância entre os dois métodos é devida ao erro de arredondamento.
Passo 4
Para resolvermos a letra temos que lebrar desse conceito aqui:
A taxa de transferência de calor de uma única aleta é simplesmente a soma da transferência de calor dos elementos nodais, ou seja:
Realizando o somatório, temos...
Como possuímos todos os valores, consuimos chegar no seguinte resultado:
Porém o exercício nos pede para comparar esse valor com a solução analítica, lembra que citei que nossa aleta é uma aleta convectiva? Certo ela também terá uma equação para taxa de transferência de calor que é dada por:
Logo,
Resposta
Ei, a resposta está no passo a passo :)