Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 17

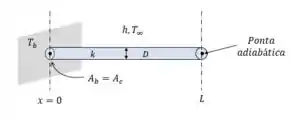
Uma aleta de alumínio cilíndrica com ponta adiabática está fixada em uma parede com temperatura de superfície de 300 ° C , exposta condição do ar ambiente de 15 ° C , com coeficiente de transferência de calor por convecção de 150 W m 2 ∙ K . A aleta tem seção transversal uniforme com diâmetro de 1   c m , comprimento de 5   c m e condutividade térmica de 237 W m ∙ K . Suponha transferência de calor constante unidimensional ao longo da aleta e espaçamento nodal uniforme de 10   m m e a seguir ( a ) obtenha as equações de diferenças finitas para uso com método iterativo de Gauss-Seidel e ( b ) determine as temperaturas nodais usando o método iterativo de Gauss-Seidel e compare os resultados com a solução analítica.

Passo 1

Bora lá pessoal, como primeiro passo nós temos que extrair os dados do enunciado, eu separei aqui pra você, olha só:

D = 1   c m   ; L = 5   c m ; T b = 300 ; T ∞ = 15 ° C ;   k = 237 W m ∙ k ; h =   150 W m 2 ∙ k   ;   ∆ x = 10   m m

Beleza! Agora precisamos encontrar o número de nós na direção m que a nossa aleta terá, basta usarmos essa equação:

m = L ∆ x + 1 = 5 1 + 1 = 6

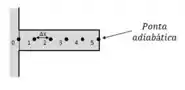
Para ficar mais visível, podemos planificar nossa aleta e acrescentar os nós, onde o nó 0 equivale a T b = 300 ° C , lembre-se que nossa aleta possui ponta adiabática:

Passo 2

Agora precisamos expressar a formulação para diferenças finitas para os nós 1, 2, 3 e 4, a equação geral e dada por...

k A T m - 1 - T m ∆ x + k A T m + 1 - T m ∆ x + h p ∆ x T ∞ - T m = 0

Vamos diminuir essa equação enorme? Basta dividirmos tudo por k A ∆ x , ela fica assim:

T m - 1 - 2 T m + T m + 1 + h p ∆ x 2 k A T ∞ - T m = 0

Isolando para T m …

T m = 2 + h p ∆ x 2 k A - 1 T m - 1 + T m + 1 + h p ∆ x 2 k A T ∞

Onde,

h p ∆ x 2 k A = 4 h ∆ x 2 k D = 4 ∙ 150 ∙ 0,01 2 237 ∙ 0,1 = 0,002197

Note que o nó 5 se encontra na extremidade da aleta, logo sua equação ficara um pouco diferente, mas fica tranquilo...só precisamos considerar que sua ponta é adiabática, logo:

2 k A T 4 - T 5 ∆ x + h p ∆ x T ∞ - T 5 = 0

T 5 = 2 + h p ∆ x 2 k A - 1 2 T 4 + h p ∆ 2 k A T ∞

Passo 3

Muito bem! Agora vamos equacionar os pontos e assim responder a letra ( a ) ...

m 1 → T 1 = 0,4938 T 0 + 0,4938 T 2 + 0,1875

m 2 → T 2 = 0,4938 T 1 + 0,4938 T 3 + 0,1875

m 3 → T 3 = 0,4938 T 2 + 0,4938 T 4 + 0,1875

m 4 → T 4 = 0,4938 T 3 + 0,4938 T 5 + 0,1875

m 5 → T 5 = 0,9876 T 4 + 0,1875

Para respondermos a letra b precisamos resolver as equações acima...mas antes precisamos admitir um valor inicial para as temperaturas nodais para realizar as interações, nós podemos iniciar com uma temperatura menor do que a da parede, como por exemplo T 1 = T 2 = T 3 = T 4 = T 5 = 250 ° C .

Logo realizando os cálculos a partir das equações anteriores:

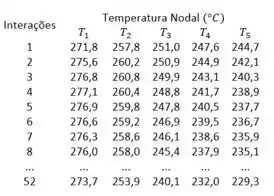
T 1 = 273,7 ° C ;   T 2 = 253,9 ° C ;   T 3 = 240,1 ° C ;   T 4 = 232,0 ° C ; T 5 = 229,3 ° C

Note que o exercício se trata de uma aleta, logo precisamos de uma equação que nos de a variação de temperatura ao longo da aleta, porém temos que tomar cuidado, pois se trata de uma aleta com ponta adiabática que significa que sua em sua ponta não realiza convecção, logo a equação que queremos é essa aqui:

T x - T ∞ T b - T ∞ = cosh ⁡ m ( L - x ) cosh ⁡ m L

m = 4 h k D

Com essa equação podemos calcular a temperatura em cada ponto ao longo da aleta e comparar com os valores numéricos:

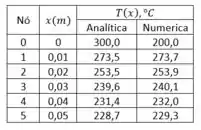
A diferença entre os dois resultados é decorrente da natureza aproximada da análise numérica, porém os valores deram próximos não? A pequena discrepância entre os dois métodos é devida ao erro de arredondamento.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro