Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 128

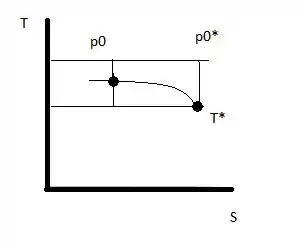
Ar é aspirado da atmosfera ( 20 º C   e   101   k P a ) através de um bocal convergente para o interior de um tubo de área constante, longo e termicamente isolado com diâmetro de 20   m m . O escoamento no bocal é isentrópico. A pressão na entrada do tubo de área constante é p 1   =   99,4   k P a . Avalie a vazão mássica através do tubo. Calcule T * e p * para o processo isentrópico. Calcule T *   e p * para o escoamento saindo do tubo de área constante. Mostre os pontos correspondentes do estado de estagnação e estático sobre um diagrama   T s .

Passo 1

Fala aí, galera. Vamos para mais um problema de mecânica dos fluidos. Primeiramente, sabemos que:

T 0 T = 1 + k - 1 2 M 2

p = ρ R T

m ˙ = ρ V A

p 0 P = T 0 T k k - 1

Assumindo um fluxo isentrópico no bico:

T 01 = T 0

p 01 = p 0

T 1 = T 0 1 + k - 1 2 M 2 - 291,7 K

Calculando o número de Mach:

M 1 = 0,151    

Logo:

V 1 = M 1 C 1 = 51,7 m s

m ˙ = 0,0193 k g s

Finalmente:

T * = T 0 1 + k - 1 2 M 2 = 244 K

p * = p 0 T 0 T k k - 1 = 53,4 k P a

Passo 2

Já para o escoamento saindo de um tubo com área constante:

T * = 244 K

Pela continuidade:

ρ 1 V 1 = ρ 2 V 2

ρ * = 0,1949   k g / m ³

Logo:

p * = ρ * R T * = 13,6 k P a

Passo 3

Já o comportamento, é dado pelo gráfico:

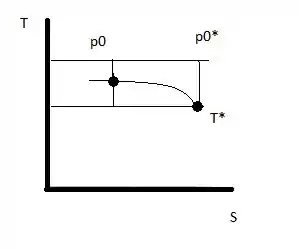
Resposta

T * = 244 K

p * = 53,4 k P a

T * = 244 K

p * = 13,6 k P a

Ver Outros Exercícios desse livro