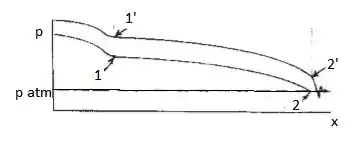
Ar escoa através de um bocal convergente e em seguida em um comprimento de um tubo termicamente isolado. O ar é fornecido de um tanque onde a temperatura permanece constante a e a pressão é variável. A extremidade de saída do tubo descarrega para a atmosfera. Quando o escoamento de saída está bloqueado, medições de pressão mostram que a pressão e o número de Mach na entrada do tubo são, respectivamente, e 0,30. Determine a pressão e a temperatura no tanque, a pressão de estagnação, e a vazão mássica do escoamento de saída, se o diâmetro do tubo for . Mostre em um diagrama o efeito do aumento da pressão do tanque até . Esboce um gráfico com a distribuição de pressão em função da distância ao longo do canal para esta nova condição de escoamento.

Passo 1

Passo 2

Passo 3

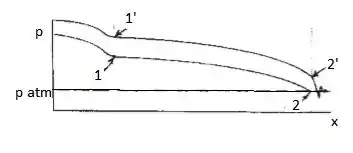
Resposta