Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 88

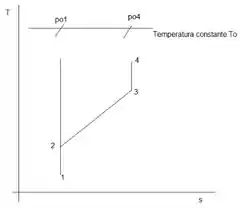
Um avião supersônico voa a M 1 = 2,7 a 20   k m de altitude em um dia-padrão. Ar é desacelerado isentropicamente pelo sistema de admissão do motor para M 2 = 1,3 . UM choque normal ocorre nesse local. O escoamento subsônico resultante é desacelerado ainda mais para M 4 = 0,4 . O processo de difusão subsônica é adiabático, mas não é isentrópico; a pressão final é 104   k P a   a b s . Avalie a a temperatura de estagnação do escoamento, b a variação de pressão através do choque, c a variação de entropia, s 4 - s 1 , e d a pressão final de estagnação. Esboce o processo em um diagrama T s , indicando todos os estados de estagnação e estáticos.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Dos apêndices, temos que. Para Mach M = 2,7 , temos que:

T 0 T 1 = 2,458

T = 533   K

A relação de pressão é dada por:

P 0 P 1 = 23,283

P = 128,8   k P a

Para M = 1,3 , temos que:

T 0 T 1 = 1,338

T = 398   K

A relação de pressão é dada por:

P 0 P 1 = 2,771

P = 46,48   k P a

Para M = 0,4 , temos que:

T 0 T 1 = 1 , 191

T = 474   K

A relação de pressão é dada por:

P 0 P 1 = 0,9794

P = 83,9   k P a

Passo 2

Entre os pontos 3 e 2 teremos a seguinte relação:

P 3 - P 2 = 83,9 - 46,5 = 37,4   k P a

Da equação de Gibbs, temos que:

T d s = d h - v d p

d s = c d T T - R d p p

Então entre os pontos 4 e 1 , temos que:

P 04 P 4 = 1,47

P 4 = 116   k P a

Logo:

s 4 - s 1 = c ln ⁡ T 04 T 01 - R ln ⁡ P 04 P 01

s 4 - s 1 = - 30,5 J k g ⋅ K

O gráfico T s é dado por:

Resposta

a )   T = 474   K

b )   P 3 - P 2 = 37,4   k P a

c )   s 4 - s 1 = - 30,5 J k g ⋅ K

Ver Outros Exercícios desse livro