Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 89
Uma onda de choque, originada de uma explosão, propagasse para fora. Para raios grandes, a curvatura é pequena e a onda pode ser tratada como um choque normal forte. (Os aumentos de pressão e de temperatura associados à onda de choque diminuem à medida que a onda se propaga para fora.) Em um dado instante, a frente de onda viaja a com relação ao ar não perturbado na condição padrão. Determine a velocidade do ar atrás da onda de choque com respeito à onda e a velocidade do ar atrás da onda de choque como visto por um observador sobre o solo. Desenhe um diagrama para o processo como visto por um observador sobre a onda, indicando os pontos dos estados estáticos e de estagnação e os valores das propriedades.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
No estado , temos que:
Para , do apêndice , temos que:
Passo 2
A onda se move para a direita em uma velocidade de e o ar se move para a esquerda a .
A velocidade absoluta será:
Relativamente ao piso sendo que o ar se move para a direita.
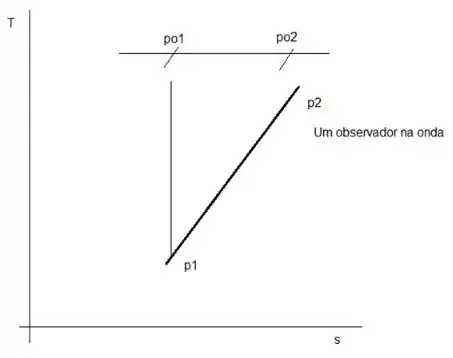
O gráfico é dado por:
