Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 178
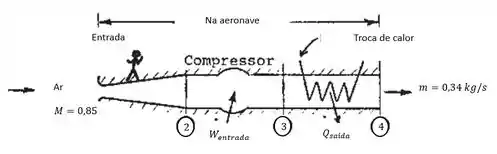
Um avião de transporte a jato voa a em uma altitude de . O ar para o sistema de pressurização da cabine é insuflado através de um duto de admissão e desacelerado isentropicamente para em relação à aeronave. Em seguida, ele entra em um compressor onde sua pressão é elevada, adiabaticamente, a fim de criar uma pressão na cabine equivalente a uma altitude de . O aumento de temperatura do ar através do compressor é de . Finalmente, o ar é resfriado para (em um trocador de calor com atrito desprezível) antes de ser lançado no interior da cabine. Esquematize um diagrama do sistema, assinalando todos os componentes e numerando apropriadamente as seções. Determine as temperaturas e as pressões estáticas e de estagnação em cada seção. Trace, em escala, um diagrama, mostrando os pontos dos estados de estagnação e estáticos e indicando os caminhos do processo. Avalie o trabalho fornecido ao compressor e a energia rejeitada no trocador de calor.
Passo 1
Fala aí galera, bora pra mais uma questão de Mecânica dos fluidos para tirarmos aquele notão na prova. Primeiro, a partir da atmosfera padrão, em , . Temos que a velocidade do som em é dada por:
E para a velocidade, temos:
Passo 2
Agora, para uma desaceleração isentrópica, temos:
Com isso, para uma desaceleração isentrópica, temos que . Portanto, a pressão em é dada por:
Então, temos que o compressor eleva o ar o equivalente a . Logo:
Por fim, assumindo que , temos:
Com isso, podemos concluir que as temperaturas serão:
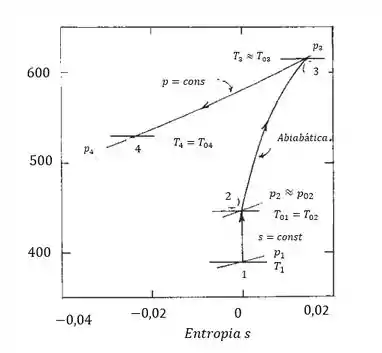
E por fim, nosso gráfico pode ser calculado através das entropias. Temos:
Portanto, nosso esboço fica assim:
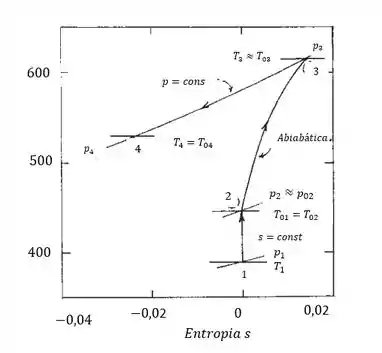
Resposta
