Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 179
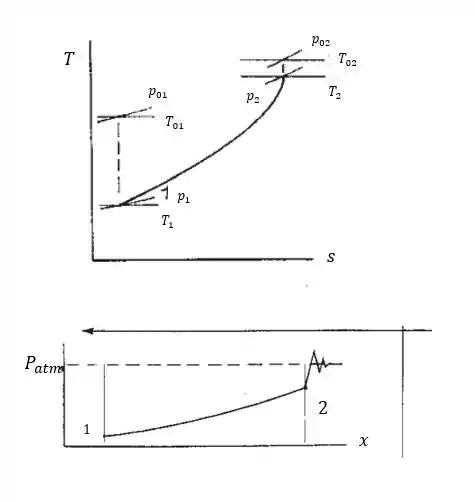
Um escoamento de ar sem atrito em um duto de área constante é descarregado à pressão atmosférica na seção . A montante, na seção , , e . Entre as seções e , de ar são adicionados ao escoamento. Determine e . Além de um diagrama para o processo, esboce a distribuição de pressão como uma função da distância ao longo do canal, assinalando as seções e .
Passo 1
Fala aí galera, bora pra mais uma questão de Mecânica dos fluidos para tirarmos aquele notão na prova. Temos que o número mínimo possível de mach para fluxo supersônico com aquecimento é dado por . Logo:
Para , temos:
Com isso, podemos calcular , fica assim:
Então, podemos calcular a pressão na seção assim:
Substituindo:
Passo 2
Agora, temos que ; ; :
E para :
Com isso, substituindo nas razões anteriores, podemos obter atráves da fórmula abaixo:
Passo 3
Por fim, temos o esboço do diagrama para o processo, esboce a distribuição de pressão como uma função da distância ao longo do canal, respectivamente, temos:
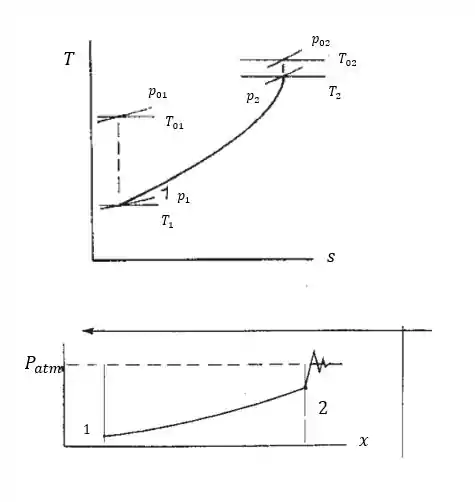
Resposta
