Em um bocal convergente/divergente escoa ar (), proveniente de um reservatório de grandes dimensões. Numa seção do divergente, nota-se uma onda de choque e, no restante do conduto, supõe-se que o escoamento seja isentrópico. A relação entre a pressão e a pressão do escoamento .............. a montante da onda de choque é 0,272. Dados: para a saída
- A intensidade da onda de choque
- Se
- As propriedades de estagnação a montante da onda de choque;
- A vazão em massa em função da área de saída;
- O esboço do diagrama do número de mach em função do comprimento do bocal;
- A irreversibilidade da onda de choque (
Passo 1
Utilizando os dados da questão, podemos utilizar a tabela 1 e tabela 2 para encontrar os valores que faltam:
Passo 2
Item a)
A intensidade de uma onda de choque é dada por:
Fazendo manipulações matemáticas, podemos dizer que:
Aplicando os valores:
Passo 3
Item b)
Nós temos os valores:
Aplicando os valores encontrado nas tabelas:
Confirmando que
Passo 4
Item c)
O item pede as propriedades de estagnação y
Para calcular a área podemos fazer algumas manipulações matemáticas:
Consultando a Tabela 1 e interpolando:
E agora vamos calcular os valores:
Passo 5
Item d)
Para calcular a vazão de massa precisaremos da densidade, que pode ser calculada pela lei dos gases ideais:
E precisaremos também da velocidade:
E agora podemos calcular a vazão mássica:
Passo 6
Item f)
Vamos calcular a entropia do sistema pela equação 12.88
Passo 7
Item e) Vamos agora desenhar os diagramas do número de Mach.
No ponto exato da saída do reservatório não há movimento. Então o número de mach é zero:
Os demais pontos foram calculados
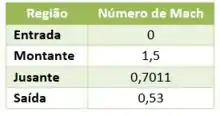
Utilizando o Excel podemos plotar esses pontos:
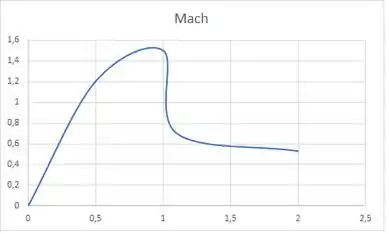
Resposta
- Sim
- ; ;