Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 12.Exercício - Ex. 25

Para o bocal convergente/divergente da figura:

  1. Quais são os valores da pressão de saída que permitem obter um escoamento totalmente isentrópico bloqueado?
  2. Qual é a máxima vazão em massa?

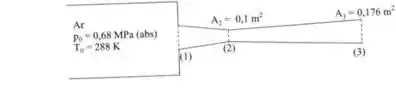
Passo 1

A garganta em (2) tem valor de mach igual a um. Logo a área (2) é a área crítica. Podemos usar isso para determinar as propriedades do ponto (3):

A 3 A * = 0,176 0,1 = 1,76

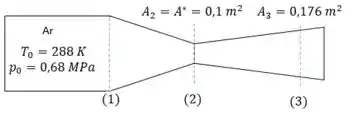
Observando a Tabela 1, encontraremos uma situação de escoamento subsônico e outra com escoamento supersônico.

Passo 2

Para situação subsônica

p 3 s u b p 0 = 0,9143 ⇒ p 3 s u b = 0,9143 ⋅ p 0 = 0,9143 ⋅ 0,68

p 3 s u b = 0,622   M P a

Para situação supersônica:

p 3 s u p e r p 0 = 0,1164 ⇒ p 3 s u p e r = 0,1164 ⋅ p 0 = 0,1164 ⋅ 0,68

p 3 s u p e r = 0,08   M P a

Passo 3

Vamos calcular a vazão em massa com base na situação crítica:

M G = 1

Pela tabela 1:

T G T 0 = 0,8333 ⇒ T G = 0,8333 ⋅ T 0 ⇒ T G = 240   K

p G p 0 = 0,5283 ⇒ p G = 0,5283 p 0 ⇒ p G = 0,359   M P a

Pela lei dos gases podemos determinar a densidade:

ρ G = p G R T G = 0,359 ⋅ 10 6 287 ⋅ 240 ⇒ ρ G = 5,21 k g s

Calculamos também a velocidade:

v G = M G k R T G = 1 ⋅ 1,4 ⋅ 287 ⋅ 240 ⇒ v G = 310,5 m s

Com esses dados podemos calcular a vazão mássica:

Q m = �� G ⋅ v G ⋅ A G

Q M = 5,21 ⋅ 310,5 ⋅ 0,1

Q m = 162 k g s

Resposta

  1. p 3 s u b = 0,622   M P a p 3 s u p e r = 0,08   M P a
  2. Q m = 162 k g s
Ver Outros Exercícios desse livro