Um túnel aerodinâmico é projetado para uma vazão de ar de 6,3 kg/s. O número de Mach na seção de testes deverá ser igual a 2, quando a pressão e a temperatura de estagnação forem, respectivamente, 0,1 Mpa (abs) e 260 K. Calcular a área da garganta, a de saída e as pressões, temperaturas e velocidades nessas seções, considerando o escoamento isentrópico.

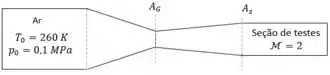
Para a garganta temos:

Pela tabela 1 podemos determinar a pressão e temperatura:

Com a temperatura e pressão podemos calcular a densidade do ar:

Com a temperatura podemos calcular a velocidade:

E como temos a vazão mássica podemos calcular a área crítica: