Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 159

Um bocal venturi moderno é calibrado em um escoamento de laboratório com água a 20°C. O diâmetro do tubo é 5,5 cm, e o diâmetro da garganta do venturi é 3,5 cm. A vazão é medida por meio de um tanque de pesagem e a queda de pressão por meio de um manômetro de água e mercúrio. A vazão em massa e as leituras manométricas são as seguintes:

Use esses dados para plotar uma curva de calibração do coeficiente de descarga do venturi em função do número de Reynolds. Compare com a correlação aceita, equação 6.114

Passo 1

E ai, galera! Tranquilidade? Bora que bora encarar mais um desafio?

Vamos obter os valores das propriedades da água na temperatura dada!!

ρ = 998 k g m 3

μ = 0,001 k g m . s

Bem, note que podemos converter a vazão mássica e a altura manométrica dada em coeficiente de descarga e no número de Reynold de forma super simples:

Q = m ˙ 998 = C d π 4 0,035 2 2 13,56 - 1 ρ á g u a 9,81 h ρ á g u a 1 - 3,5 5 4

C d = m ˙ 16,485 h

R e D = 4 m ˙ π D μ = 4 m ˙ π 0,001 0,055 = 23150 m ˙

Passo 2

Note que deixamos todo o nosso equacionamento em função das variáveis dadas, certo? Então podemos agora escrever uma nova tabela para cada uma das nossas equações e substituir os valores, obtendo o seguinte:

Passo 3

Plotando o gráfico de Reynold por coeficiente de descarga, obtemos o seguinte:

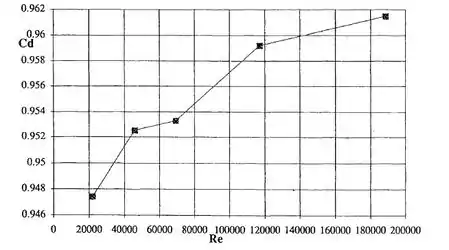
Eles lembram o clássico Venturi Herschel, mas os dados são de um Venturi moderno, o qual nós temos e sabemos apenas os valores dentro da C d dentro da faixa de 1,5   x   10 5 < R e D < 2   x   10 5 :

C d = 0,9858 - 0,196 3,5 5,5 4,5 = 0,96

Resposta

C d = 0,96

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tubo liso, de 200m de comprimento e diâmetro de 100m m , liga dois reservatórios (a entrada e a saída do tubo são de bordasvivas). No ponto médio do trecho de tubo está uma placa de orifício com di
A vazão volumétrica em um duto circular pode ser medida por um “pitot transverso”, isto é, pela medida da velocidade em vários segmentos de área através do duto, seguida do somatório das vazões segmen
Em alguns estados do oeste, água para mineração e irrigação era vendida por “polegada de mineiro”, ou seja, a taxa para a qual a água escoa através de uma abertura de 645m m 2 de área em uma tábua ver
Gasolina a 20°C escoa a 0,06m³/h por um tubo de 15 cm de diâmetro e é medida por um medidor do tipo bocal de raio longo de 9 cm. Qual é a queda de pressão esperada através do bocal?
Um avião utiliza um tubo de Pitot estático como velocímetro. As medidas, com suas incertezas são: uma temperatura estática de - 11 ± 3 ° ° C , uma pressão estática de 60 ± 2k P a e uma diferença de pr