Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 12.Problemas - Ex. 84
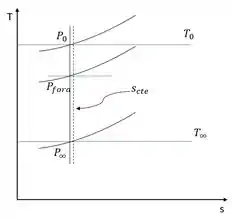
Um Boeing 747 voa a M = 0,87 em uma altitude de 13 km em um dia-padrão. Uma janela na cabine do piloto está localizada onde o número de Mach do escoamento externo é 0,2 em relação à superfície do avião. A cabine é pressurizada para uma altitude equivalente de 2500 m em uma atmosfera-padrão. Estime a diferença de pressão através da janela. Certifique-se de especificar o sentido da força de pressão resultante.
Passo 1
Oi pessoal, tudo bem ?
Primeiro, vamos relembrar as equações de estagnação pela razão de pressão e temperatura isentrópica:
Consideremos:
Obs: Propriedades do ar (Tabela A.6). ;
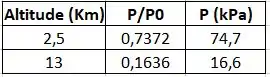
A tabela A.3 traz temperaturas equivalentes à altitude e relações da pressão com a pressão atmosférica , então, em suma:
Passo 2
A pressão de estagnação à 13 km pode ser calculada:
Para a estagnação em (altitude equivalente fora da cabine do avião):
Passo 3
Então, a diferença de pressão na janela da cabine é a diferença entre a pressão dentro (altitude de 13km) e a pressão fora (altitude equivalente de 2,5 km):
Resposta
Portanto:
