Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 114

Um choque normal ocorre em uma seção de um duto de área constante, isolado termicamente. O escoamento é com atrito. Na seção 1, a uma certa distância a montante do choque, T 1 = 260   K . Na seção 4, a uma certa distância a jusante do choque, T 4 = 417   K e M 4 = 1 . Denote as condições imediatamente antes e após o choque pelos subscritos 2 e 3, respectivamente. Esboce a distribuição de pressão ao longo do duto, indicando claramente os locais das seções de 1 a 4. Esboce um diagrama T s para o escoamento. Determine o número de Mach na seção 1.

Passo 1

Tá legal! Vamos começar representando o escoamento e a região de choque, então, conforme dito no enunciado, teremos:

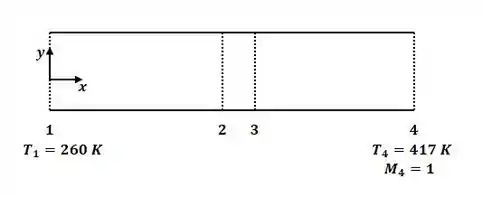
Passo 2

Agora, a distribuição de pressão será:

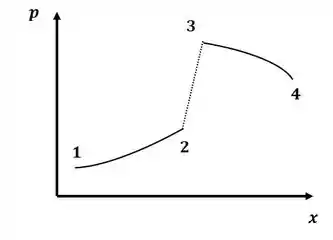
E, o diagrama T s será:

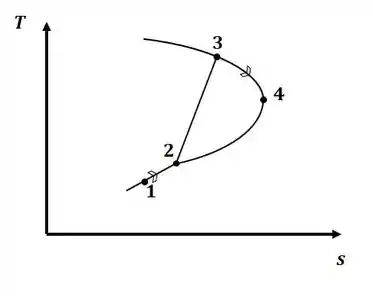
Passo 3

Para um escoamento adiabático, teremos temperatura constante, dessa forma, temos:

T 0 1 = T 0 4 = T 4 1 + k - 1 2 M 4 2

Substituindo os valores conhecidos:

T 0 1 = 417 1 + 1,4 - 1 2 1 2 → T 0 1 = 500,4   K

Então, a equação para M 1 será:

T 0 1 = T 1 1 + k - 1 2 M 1 2

Isolando M 1 temos:

T 0 1 T 1 = 1 + k - 1 2 M 1 2 → M 1 = 2 k - 1 T 0 1 T 1 - 1

Substituindo os valores conhecidos:

M 1 = 2 1,4 - 1 500,4 260 - 1 → M 1 = 2,15

Resposta

M 1 = 2,15

Ver Outros Exercícios desse livro