Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 3
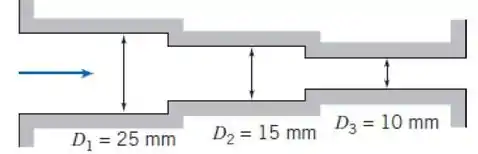
Ar a 40°C escoa em um sistema de tubos em que o diâmetro é reduzido em dois estágios de 25 mm para 15 mm e para 10 mm. Cada seção tem 2 m de comprimento. A medida que a vazão é aumentada, em qual seção o escoamento tornar-se-á turbulente primeiro? Determine as vazões nas quais uma, duas e, em seguida, as três seções tornam-se turbulentas em primeira instância. Para cada uma destas vazões, determine quais seções (se existir alguma) atingirão escoamento completamente desenvolvido.
Passo 1
Beleza! O primeiro passo nesse exercício é encontrar a expressão para a vazão nos três estágios para o sistema, para depois encontrarmos o comprimento do escoamento laminar e comparar com o comprimento total de cada seção. Dessa forma, sabemos que o número de Reynolds é dado por:
No entanto, podemos escrever a vazão como:
Substituindo essa expressão na equação de Reynolds e isolando a vazão, temos:
Agora, sabemos que o número de Reynolds crítico para esse escoamento será:
Antes de começar os cálculos, devemos ir na tabela A.8 do apêndice A do livro e pegar o valor da viscosidade cinemática para o ar a 40°C, então, teremos:
Então, agora, vamos substituir o valor dos diâmetros das tubulações para encontrar a vazão corresponde ao número de Reynolds crítico, então, teremos para as três tubulações:
Então, como poderíamos imaginar, quanto menor o diâmetro da tubulação, para as mesmas condições, teremos a turbulência ocorrendo primeiro.
Passo 2
Vamos começar nossa análise pela tubulação de menor diâmetro. Então, teremos que o comprimento laminar será dado pela equação:
Então, substituindo os valores conhecidos, lembrando que o Reynolds será o crítico, temos:
Sob essa análise, como , então o escoamento será totalmente desenvolvido. Agora analisando a relação entre comprimento mínimo e máximo, temos:
E a relação entre os dois comprimentos será:
Então, como temos , então o escoamento será totalmente desenvolvido.
Passo 3
Agora vamos repetir a análise feita no passo 2, só que para a tubulação com . Então, teremos que o comprimento laminar será dado pela equação:
Então, substituindo os valores conhecidos, lembrando que o Reynolds será o crítico, temos:
Sob essa análise, como , então o escoamento não será totalmente desenvolvido. Agora analisando a relação entre comprimento mínimo e máximo, temos:
E a relação entre os dois comprimentos será:
Então, como temos , então o escoamento será totalmente desenvolvido.
Passo 4
Agora, de novo, vamos repetir a análise feita no passo 2, só que para a tubulação com . Então, teremos que o comprimento laminar será dado pela equação:
Então, substituindo os valores conhecidos, lembrando que o Reynolds será o crítico, temos:
Sob essa análise, como , então o escoamento não será totalmente desenvolvido. Agora analisando a relação entre comprimento mínimo e máximo, temos:
E a relação entre os dois comprimentos será:
Então, como temos , então o escoamento será totalmente desenvolvido.